|
Wiki
UniCrema
Materie per semestre
Materie per anno
Materie per laurea
Help
|
|
Uni.IT-ComplessitàNelTempo History
Hide minor edits - Show changes to markup
Changed line 27 from:
Sia t:N->R+ una a funzione. Definiamo la classe di complessità nel tempo, TIME(t(n)), come l'insieme di tutti i linguaggi che sono decidibili in tempo O(t(n)) (polinomiale) da una MdT.
to:
Sia t:N->R+ una funzione. Definiamo la classe di complessità nel tempo, TIME(t(n)), come l'insieme di tutti i linguaggi che sono decidibili in tempo O(t(n)) (polinomiale) da una MdT.
Changed lines 42-43 from:
Dato che tra O(n) e O(t2(n)) il secondo è il contributo più importante, trascuriamo il primo è affermiamo che simulare una multinastro su MdT a nastro singolo richiede il quadrato del tempo di esecuzione.
to:
Dato che tra O(n) e O(t2(n)) il secondo è il contributo più importante, trascuriamo il primo è affermiamo che simulare una multinastro su MdT a nastro singolo richiede il quadrato del tempo di esecuzione della prima.
Changed line 54 from:
Per rendere più efficiente l'algoritmo, l'esplorazione dell'albero alla ricerca dello stato di accettazione non viene fatta in profondità (dalla radice alla foglia e poi da capo con un altro percorso), ma in ampiezza (controllando gli stati dei nodi livello per livello).\\
to:
Per rendere più efficiente l'algoritmo, l'esplorazione dell'albero per cercare lo stato di accettazione non viene fatta in profondità (dalla radice alla foglia e poi da capo con un altro percorso), ma in ampiezza (controllando gli stati dei nodi livello per livello).\\
Changed line 76 from:
Per dimostrare che PATH appartiene a P dovremo dimostrare che è risolvibile in tempo polinomiale. Una possibile strada è quella di partire da s e marcare tutti i nodi raggiungibili con passo 1, quindi ripetere l'operazione a partire da essi (raggiungendo una distanza da s pari a 2). L'operazione va ripetuta finché non è più possibile marcare nuovi nodi. A questo punto bisogna verificare se t è stato segnato o no: se sì PATH è vero, altrimenti no.\\
to:
Per dimostrare che PATH appartiene a P dovremo dimostrare che è risolvibile in tempo polinomiale. Una possibile strada è quella di partire da s e marcare tutti i nodi raggiungibili con passo 1, per poi ripetere l'operazione partendo da essi (raggiungendo una distanza da s pari a 2). L'operazione va ripetuta finché non è più possibile marcare nuovi nodi. A questo punto bisogna verificare se t è stato segnato o no: se sì PATH è vero, altrimenti no.\\
Changed lines 83-84 from:
3.fai una scan degli archi di G. Se trovi l'arco (a,b), dove a è un nodo marcato e b no, marca b;
to:
3.fai una scan degli archi di G. Se trovi l'arco (a,b), dove a è un nodo marcato e b no,
marca b;
Changed line 95 from:
Prima di tutto, di cosa diavolo stiamo parlando? Il problema RELPRIME è quello che deve verificare se due numeri sono primi tra loro, ovvero se il più grande intero che li divide entrambi è 1. Più formalmente:
to:
Prima di tutto, di cosa diavolo stiamo parlando? Il problema RELPRIME è quello che deve verificare se due numeri sono primi tra loro, ovvero se il più grande intero che li divide entrambi è 1. Più formalmente:\\
Changed lines 118-119 from:
Creiamo ora una seconda MdT che usa E come subroutine:
to:
Creiamo ora una seconda MdT che usa E come sub-routine:
Changed lines 142-143 from:
Sappiamo già dalle lezioni precedenti che i linguaggi liberi dal contesto (da ora CFL) sono decidibili, perché è possibile creare un algoritmo che lo decida. Dobbiamo quindi dimostrare che tale algoritmo viene eseguito in tempo polinomiale. Dov'è la fregatura? Che la dimostrazione della decidibilità di un CFL L tirava in ballo il fatto che era stato generato da una grammatica libera dal contesto G espressa nella forma normale Chomsky, e che bisognava verificare tutte le derivazioni di G per vedere se una certa stringa di L poteva essere accettata. Il numero di derivazioni è ahinoi esponenziale, quindi dobbiamo scegliere un'altra strada per dimostrare il nostro teorema.
to:
Sappiamo già dalle lezioni precedenti che i linguaggi liberi dal contesto (da ora CFL) sono decidibili, perché è possibile creare un algoritmo che lo decida. Dobbiamo quindi dimostrare che tale algoritmo viene eseguito in tempo polinomiale. Dov'è la fregatura? Che la dimostrazione della decidibilità di un CFL L tirava in ballo il fatto che era stato generato da una grammatica libera dal contesto G espressa nella forma normale di Chomsky, e che bisognava verificare tutte le derivazioni di G per vedere se una certa stringa di L poteva essere accettata. Il numero di derivazioni è però esponenziale, quindi dobbiamo scegliere un'altra strada per dimostrare il nostro teorema.
Changed line 145 from:
Nella programmazione dinamica si cercano e si utilizzano le soluzioni di sottoproblemi per risolvere il problema principale. Nel nostro caso i sottoproblemi sono le sottostringhe generate per scomposizione dall'originale stringa w generata da G, e dovremo verificare che ognuna di esse possa essere derivata a partire dalle variabili della grammatica. Per fare ciò costruiremo una tabella n x n, con coordinate i e j. In ogni cella (i,j) con i<=j potrò trovare tutte le variabili che mi permettono di generare la sottostringa wiwi+1...wj; al contrario tutte le celle con i>j saranno inutilizzate. Grazie ai principi della programmazione dinamica useremo via via le soluzioni ottenute per le sottostringhe precedenti. Come? Quando andando avanti con la risoluzione scopro che una data (i,j) potevo generarla utilizzando una sottostringa già risolta, nella cella metto quella sottostringa. Come? Ogni sottostringa di lunghezza k+1 può essere divisa in k modi possibili (ad esempio w1w2w3w4 può essere divisa in: w1|w2w3w4, w1w2|w3w4, w1w2w3|w4). Per riutilizzare le informazioni già messe in tabella basterà cercare nella mia grammatica una regola A->BC dove B mi permette di generare la parte sinistra e C la destra.\\
to:
Nella programmazione dinamica si cercano e si utilizzano le soluzioni di sottoproblemi per risolvere il problema principale. Nel nostro caso i sottoproblemi sono le sottostringhe generate per scomposizione dall'originale stringa w generata da G, e dovremo verificare che ognuna di esse possa essere derivata a partire dalle variabili della grammatica. Per fare ciò costruiremo una tabella n x n, con coordinate i e j. In ogni cella (i,j) con i<=j potrò trovare tutte le variabili che mi permettono di generare la sottostringa wiwi+1...wj; al contrario tutte le celle con i>j rimarranno inutilizzate. Grazie ai principi della programmazione dinamica useremo via via le soluzioni ottenute per le sottostringhe precedenti. Come? Quando andando avanti con la risoluzione scopro che posso generare una data (i,j) utilizzando una sottostringa già risolta, metto nella cella quella sottostringa. Come? Ogni sottostringa di lunghezza k+1 può essere divisa in k modi possibili (ad esempio w1w2w3w4 può essere divisa in: w1|w2w3w4, w1w2|w3w4, w1w2w3|w4). Per riutilizzare le informazioni già messe in tabella basterà cercare nella mia grammatica una regola A->BC dove B mi permette di generare la parte sinistra e C la destra.\\
Changed lines 160-161 from:
11. se la cella (i,k) contiene B e la cella (k+1,j) contiene C, allora metti A nella cella (i,j)
to:
11. se la cella (i,k) contiene B e la cella (k+1,j) contiene C,
allora metti A nella cella (i,j)
Changed line 10 from:
Sia M una Macchina di Touring (da ora MdT) deterministica che si ferma su ogni ingresso. Il tempo di esecuzione o complessità nel tempo di M è la funzione f: N -> N, dove f(n) è il numero massimo di passi che M impiega su ogni ingresso di lunghezza n. Se f(n) è il tempo di esecuzione di M, diciamo che M è eseguita in tempo f(n) e che M è una tempo f(n) MdT.
to:
Sia M una Macchina di Turing (da ora MdT) deterministica che si ferma su ogni ingresso. Il tempo di esecuzione o complessità nel tempo di M è la funzione f: N -> N, dove f(n) è il numero massimo di passi che M impiega su ogni ingresso di lunghezza n. Se f(n) è il tempo di esecuzione di M, diciamo che M è eseguita in tempo f(n) e che M è una tempo f(n) MdT.
Changed line 1 from:
(:title Informatica Teorica - Spazio-complessità:)
to:
(:title Informatica Teorica - Complessità nel tempo:)
Changed lines 5-15 from:
:: Informatica Teorica - Spazio-complessità ::
Appunti & Dimostrazioni del 19 Maggio
Complessità in termini di spazio
Così come è possibile quantificare la complessità di un algoritmo in funzione della risorsa tempo, si può fare lo stesso considerando la risorsa spazio, ovvero la memoria utilizzata. Per misurarla si utilizzerà una MdT M, e in particolare:
- se M è
deterministica, allora la sua spazio complessità è la funzione f(n), cioè il massimo numero di celle del nastro su cui M farà uno scan per ogni ingresso di lunghezza n;
- se M è
non deterministica (da ora, n.d.), allora la sua spazio complessità f(n) sarà il numero massimo di celle del nastro su cui M farà uno scan per ogni ramo della sua computazione e per ogni ingresso di lunghezza n.
Quella che ci interessa è però la stima asintotica della spazio-complessità, che può essere così definita:
to:
:: Informatica Teorica - Complessità nel tempo ::
Appunti & Dimostrazioni del 5 Maggio
Cenni teorici
Sia M una Macchina di Touring (da ora MdT) deterministica che si ferma su ogni ingresso. Il tempo di esecuzione o complessità nel tempo di M è la funzione f: N -> N, dove f(n) è il numero massimo di passi che M impiega su ogni ingresso di lunghezza n. Se f(n) è il tempo di esecuzione di M, diciamo che M è eseguita in tempo f(n) e che M è una tempo f(n) MdT.
Della complessità nel tempo non si dà una misura precisa, ma una stima risultante dall'analisi asintotica dell'algoritmo. In particolare introduciamo le notazioni O ("o grande") e o ("o piccolo").
Siano f e g due funzioni f,g: N -> R+. Diciamo che f(n) = O(g(n)) se esistono due interi positivi c e n0 tali che per ogni intero n>=n0:
f(n) >= c*g(n)
Quando f(n) = O(g(n)) diciamo che g(n) è un limite superiore (upper bound) per f(n), o più precisamente che g(n) è un limite superiore asintotico per f(n), per enfatizzare il fatto che stiamo ignorando le costanti.
Se O può essere definita come una funzione asintoticamente "non maggiore" di un'altra (minore o uguale), con o piccolo definiamo una funzione asintoticamente "minore" di un'altra (strettamente minore). Facendo qualche esempio:
- n = o(nlog(logn))
- nlog(logn) = o(n(logn))
- n2 = o(n3)
Perché abbiamo parlato di o grandi e o piccole? Perché quando si fa l'analisi asintotica di un algoritmo si considerano solo i termini di ordine maggiore che partecipano a formare il tempo di esecuzione complessivo, trascurando i coefficienti, le costanti e tutti i termini di grado inferiore.
Ad esempio: f(n) = 3n3 + 2n2 + n + 100 = O(n3)
Concludiamo definendo cos'è una classe di complessità nel tempo:
Changed lines 27-29 from:
Sia f:N->R+ una funzione. Le classi di spazio complessità, SPACE(f(n)) ed NSPACE(f(n)), sono definite come segue:
- SPACE(f(n)) = {L|L è un linguaggio deciso da una MdT deterministica O(f(n))-spazio}
- NSPACE(f(n)) = {L|L è un linguaggio deciso da una MdT
n.d. O(f(n))-spazio}
to:
Sia t:N->R+ una a funzione. Definiamo la classe di complessità nel tempo, TIME(t(n)), come l'insieme di tutti i linguaggi che sono decidibili in tempo O(t(n)) (polinomiale) da una MdT.
Changed lines 30-38 from:
Esempio 1: SAT è spazio-lineare?
Sappiamo che il problema SAT è NP-completo, e che quindi non può essere risolto con una MdT deterministica in tempo polinomiale. Figurarsi se ci riesce in tempo lineare. Lo spazio ha però una caratteristica in più rispetto al tempo: può essere riutilizzato!
L'idea per la nostra MdT che risolve il problema SAT in spazio lineare, è quella di assegnare una cella ad ogni variabile, e riutilizzarla ogni volta che facciamo un nuovo assegnamento:
M = "su ingresso Φ: (dove Φ è una formula booleana)
1. per ogni valore di verità assegnato alle variabili x 1..x n di Φ:
2. valuta Φ sull'assegnamento;
3. se Φ=1 in almeno un assegnamento, allora ACCETTA; altrimenti RIFIUTA."
to:
Teorema 1 - sulle relazioni di complessità tra modelli
Sia t(n) una funzione, con t(n)>=n. Ogni MdT multinastro t(n)-tempo ha una equivalente MdT a nastro singolo O(t2(n))-tempo.
Deleted lines 35-62:
M è evidentemente spazio-lineare, perché ad ogni iterazione utilizza sempre lo stesso spazio in memoria, lineare al numero di variabili. Dato che tale numero è al più pari ad n, la lunghezza dell'ingresso, allora possiamo dire che la macchina è eseguita in O(n)-spazio.
Esempio 2: (not)ALL è spazio-lineare?
Consideriamo ora un problema risolvibile con una MdT n.d., il problema ALLNFA, che deve stabilire se un determinato linguaggio accetta tutte le stringhe. Più formalmente:
ALLNFA = {<A> | A è un NFA ed L(A)=Σ*}
A noi non interessa il problema ALLNFA, ma il suo complementare, di cui vogliamo trovare una MdT n.d. spazio-lineare che lo risolva. L'idea è quella di usare il non determinismo per trovare una stringa che sia rifiutata dall'NFA, ed usare uno spazio lineare per tenere traccia degli stati in cui l'automa può trovarsi in un determinato momento. Lineare a cosa? Semplice: al numero q di stati in cui può trovarsi l'NFA, di cui ricordiamo possono esserne contemporaneamente attivi 2q, ognuno rappresentato con un simbolo.
Scriviamo la MdT N:
N = "su ingresso <M>: (dove <M> è un NFA)
1. metti un marker sullo stato iniziale dell'NFA;
2. ripeti 2 q volte:
3. seleziona in modo n.d. un simbolo d'ingresso e aggiorna le posizioni dei marker sugli stati di M;
4. se nessun marker è su uno stato accettante, allora ACCETTA; altrimenti RIFIUTA."
Si noti che il passo 3 non fa altro che simulare la lettura del simbolo selezionato in modo n.d..
Per come è stato costruito N, l'unico spazio di cui ha bisogno è quello per memorizzare le posizioni dei marker e per il contatore del ciclo descritto ai passi (2) e (3). Si tratta quindi di uno spazio lineare all'ingresso, perché ad ogni iterazione andrò a scrivere sempre sulle stesse celle di memoria!
Teorema di Savitch
La MdT deterministica che simula la corrispondente n.d. ha una complessità tempo esponenziale rispetto al suo modello. Il teorema di Savitch dimostra invece che nello spazio la complessità non aumenta allo stesso modo, ma molto meno.
Per ogni funzione f:N->R+, dove f(n)>=n,
Changed lines 38-51 from:
La situazione: partiamo con una MdT n.d. f(n)-spazio, e dobbiamo simularla in modo deterministico sapendo che con quella si potranno avere più scelte per ogni nodo.
Una prima idea è simulare tutti i possibili rami della n.d., ma così facendo non potremo sovrascrivere l'area di memoria utilizzata, perché dobbiamo tenere traccia di quale ramo termina e quale no; con questa strategia si userebbe quindi uno spazio esponenziale, e non va bene.
La soluzione è introdurre un nuovo problema, quello che ci permette di verificare se una MdT n.d. può passare da una configurazione iniziale c1 a quella finale c2 in un numero di passi minore o uguale a t. Chiamiamo questo secondo problema yieldability problem, e lo risolviamo definendo la MdT deterministica e ricorsiva CANYIELD.
Arriviamo al dunque.
Data una MdT n.d. N che decide un linguaggio A in uno spazio f(n), costruiamo la MdT deterministica M che utilizzando la procedura CANYIELD riesce a decidere A. N avrà come input la stringa w da verificare, mentre CANYIELD riceverà in ingresso le due configurazioni c1 e c2 , ed il numero massimo di passi impiegabili t.
CANYIELD = "su ingresso c1, c2, t:
- se t=1, verifica se c1=c2 o se c1->c2 in un unico passo in accordo alle regole di N. Se uno dei due test va a buon fine, ACCETTA; altrimenti RIFIUTA;
2. se t>1, per ogni configurazione c m di N su w che usa spazio f(n);
3. esegui CANYIELD su ingresso c1, cm, t/2;
4. esegui CANYIELD su ingresso cm, c2, t/2;
5. se (3) e (4) vanno entrambi a buon fine, allora ACCETTA; altrimenti RIFIUTA."
to:
Consideriamo M una MdT con k nastri, ed S la corrispondente MdT a nastro singolo. S è costruita copiando i contenuti dei k nastri sul suo mettendoli in fila uno dopo l'altro e separandoli con un #. Perché S riesca a simulare un singolo passo di M su un certo nastro, dovrà prima posizionare la propria testina sul punto corrispondente, e solo dopo compiere l'operazione. Sappiamo dal testo del teorema che nel peggiore dei casi la testina di M impiegherà t(n) tempo per raggiungere il punto desiderato e compiere l'operazione, quindi avrà complessità O(t(n)). La complessità di S sarà dunque data dai contributi derivanti dalle seguenti operazioni:
- ricopiare correttamente il contenuto di M, impiegando O(n) passi
- simulare M su nastro singolo, impiegando t(n) passaggi ognuno con complessità O(t(n)). Ovvero: t(n)*O(t(n))=O(t2(n))
Dato che tra O(n) e O(t2(n)) il secondo è il contributo più importante, trascuriamo il primo è affermiamo che simulare una multinastro su MdT a nastro singolo richiede il quadrato del tempo di esecuzione.
Teorema 2 - sulle relazioni di complessità tra modelli
Sia t(n) una funzione, con t(n)>=2. Ogni MdT a singolo nastro non-deterministica t(n)-tempo ha una equivalente MdT a nastro singolo deterministica 2O(t(n))-tempo.
Changed lines 51-55 from:
Passiamo ora a definire la MdT M che simula N, e per farlo introduciamo alcuni accorgimenti:
- quando N accetta pulisce l'intero contenuto del nastro e lo sostituisce con la configurazione caccept;
- chiamiamo cstart la configurazione iniziale di N sulla stringa d'ingresso w;
- selezioniamo una costante d tale che N non abbia un numero di configurazioni maggiore di 2d*f(n), dove n è la lunghezza di w. In questo modo fissiamo un limite superiore al tempo di computazione per ogni ramo, e creiamo un legame tra numero di configurazioni possibili e tempo.
to:
Dimostrazione
Data una MdT non deterministica N con tempo di esecuzione t(n), sappiamo che è possibile creare una MdT deterministica D equivalente che intraprende ogni possibile ramo della computazione non deterministica. In particolare, dato un ingresso di lunghezza n (la grandezza della stringa w) ogni ramo dell'albero di computazione non deterministica di N avrà al massimo lunghezza t(n). Supponendo che ogni nodo possa avere al massimo b figli (ovvero le scelte legali della funzione di transizione), avremo al massimo bt(n) foglie.
Per rendere più efficiente l'algoritmo, l'esplorazione dell'albero alla ricerca dello stato di accettazione non viene fatta in profondità (dalla radice alla foglia e poi da capo con un altro percorso), ma in ampiezza (controllando gli stati dei nodi livello per livello).
Il numero di nodi nell'albero è di poco inferiore al doppio delle foglie, quindi possiamo dare come limite superiore al numero di nodi O(bt(n)). A questo punto, sapendo che il tempo di esplorazione dalla radice a qualunque nodo è pari a O(t(n)), e che nel caso peggiore bisognerà visitare tutti gli O(bt(n)) nodi dell'albero, il tempo totale di esecuzione dell'algoritmo D è pari a:
O(t(n)*bt(n)) = 2O(t(n))
Facciamo qualche considerazione conclusiva sull'equivalenza O(t(n)*bt(n))=2O(t(n)):
- si tratta di un prodotto tra un polinomio e un'esponenziale, ed avendo quest'ultimo un ordine di grandezza maggiore, è possibile trascurare il primo e considerare come complessità dell'algoritmo solo O(bt(n))
- per una serie di motivi che non ci interessano (che riguardano comunque la teoria della complessità), è possibile passare da O(bt(n)) a O(2t(n))
- siccome la base 2 è una costante, possiamo portare in alto l'o grande: O(2t(n))=2O(t(n))
Il teorema sembra già dimostrato, ma in realtà non va dimenticato che la D che simula N non è più una MdT a singolo nastro, ma per costruzione ne ha 3. Poco male: dal Teorema 1 sopra riportato sappiamo che ogni MdT multinastro t(n)-tempo ha una equivalente MdT a nastro singolo O(t2(n))-tempo. Quindi:
(2O(t(n)))2 = 2O(2t(n)) = 2O(t(n))
Dimostrazione conclusa.
Classe P
Introduciamo ora la classe P, ovvero la classe dei linguaggi che sono decidibili in tempo polinomiale su una MdT deterministica a singolo nastro. Si tratta di una classe matematicamente robusta, che non dipende quindi dal modello computazionale che sceglieremo per risolvere il problema.
I problemi in P, o tempo-polinomiali, sono una classe di problemi realisticamente risolvibili con un calcolatore. Per dimostrare che un problema è tempo-polinomiale bisognerà prima dare un limite polinomiale superiore (in notazione O grande) per il numero di passi che l'algoritmo usa per un ingresso di lunghezza n, poi esaminare ogni passo della descrizione dell'algoritmo per assicurarci che ogni passo sia tempo-polinomiale.
PATH è P?
Dato un grafo diretto G, il problema PATH ha come obiettivo quello di determinare se esiste un percorso diretto tra due nodi s e t. Più formalmente:
PATH = {<G,s,t> | G è un grafo diretto che ha percorso diretto tra s e t}
Per dimostrare che PATH appartiene a P dovremo dimostrare che è risolvibile in tempo polinomiale. Una possibile strada è quella di partire da s e marcare tutti i nodi raggiungibili con passo 1, quindi ripetere l'operazione a partire da essi (raggiungendo una distanza da s pari a 2). L'operazione va ripetuta finché non è più possibile marcare nuovi nodi. A questo punto bisogna verificare se t è stato segnato o no: se sì PATH è vero, altrimenti no.
Costruiamo ora la MdT deterministica M che implementa l'algoritmo:
Changed lines 80-81 from:
M = "su ingresso w:
- restituisci il risultato di CANYIELD(cstart, caccept,2d*f(n))."
to:
M = "su ingresso <G,s,t>:
1. marca s;
2. ripeti finché non abbiamo nuovi nodi da marcare:
3.fai una scan degli archi di G. Se trovi l'arco (a,b), dove a è un nodo marcato e b no, marca b;
4. se t è marcato, allora ACCETTA; altrimenti RIFIUTA."
Changed lines 87-98 from:
Dato che CANYIELD risolve sicuramente l'yieldability problem, possiamo affermare che M simula correttamente N. Non ci resta che fare l'analisi dell'algoritmo, e verificare se M è eseguito in O(f2(n)) spazio, come sostiene il teorema. Cosa dobbiamo fare? Calcolare quanto spazio richiede ogni ricorsione di CANYIELD e moltiplicarlo per il numero di ricorsioni stesse.
Ogni volta che CANYIELD invoca sé stesso ricorsivamente, memorizza il numero di stato corrente e i valori di c1 c2 e t su uno stack, così che possano essere ripristinati una volta tornati dalla chiamata ricorsiva. Ogni livello di ricorsione richiede quindi uno spazio addizionale O(f(n)).
Considerato che ad ogni ricorsione dimezziamo il numero di passi impiegabili t, e che inizialmente t è pari a 2d*f(n), il numero di ricorsioni è:
O(log2d*f(n)) = O(d*f(n)) = O(f(n))
Quindi, spazio richiesto ad ogni ricorsione per il numero di ricorsioni:
O(f(n)) * O(f(n)) = O(f2(n)), come sostenuto dal teorema di Savitch.
Classe PSPACE e PSPACE-completezza
PSPACE è la classe di linguaggi decidibili in spazio polinomiale usando una MdT deterministica. In altre parole:
to:
Facciamo l'analisi dell'algoritmo:
- i passi (1) e (4) sono ripetuti una sola volta
- i passi (2) e (3) (il loop) sono eseguiti m volte, dove m è il numero di nodi
Quindi, dato che il numero di passi è 1+1+m e che ognuno di essi ha complessità polinomiale, PATH è in P.
RELPRIME è P?
Prima di tutto, di cosa diavolo stiamo parlando? Il problema RELPRIME è quello che deve verificare se due numeri sono primi tra loro, ovvero se il più grande intero che li divide entrambi è 1. Più formalmente:
RELPRIME = {<x,y> | x e y sono primi tra loro}
Per dimostrare che RELPRIME appartiene a P dobbiamo trovare una MdT deterministica che lo risolva in tempo polinomiale. Iniziamo a scrivere una MdT che calcoli il divisore maggiore dati due interi x e y:
E = "su ingresso <x,y>:
1. ripeti finché y=0;
2. assegna a x il valore x mod y;
3. scambia x e y;
4. output: x"
Changed lines 107-115 from:
Analogamente, NPSPACE sarà la classe di linguaggi decidibili in spazio polinomiale usando una MdT n.d.. Si noti che per il teorema di Savitch è possibile simulare una MdT deterministica spazio-polinomiale con una MdT n.d. anch'essa spazio-polinomiale. Quindi possiamo affermare che NPSPACE=PSPACE, al contrario di quanto avviene per la tempo-complessità.
Per quanto riguarda la completezza, possiamo affermare che:
Un linguaggio B è PSPACE-completo se soddisfa due condizioni:
- B è in PSPACE;
- Ogni A in PSPACE è riducibile in tempo polinomiale a B.
Se B soddisfa solo la seconda condizione è chiamato PSPACE-hard.
to:
Facciamo un esempio di risoluzione. Dati in ingresso x=24 e y=18:
(1)
(2) x = 24 mod 18 = 6
(3) x = 18 , y = 6
(1) y=0? NO
(2) x = 18 mod 6 = 0
(3) x = 6 , y = 0
(1) y=0? SÌ
(4) output: 6
Creiamo ora una seconda MdT che usa E come subroutine:
R = "su ingresso <x,y>:
- esegui E su ingresso <x,y>;
- se il risultato è 1, allora ACCETTA; altrimenti RIFIUTA."
Changed lines 125-137 from:
Perché parliamo di tempo riducibilità e non di spazio riducibilità? Ma per non complicarci troppo la vita, belin! Life is too short! (i problemi completi sono i più difficili di tutti, ed una volta che abbiamo verificato che è in PSPACE chi se ne frega se consideriamo la riducibilità nel tempo o nello spazio)
Teorema 1 - TQBF è PSPACE-completo?
Una "formula booleana" è un'espressione che contiene variabili booleane, costanti 0 e 1, e gli operatori booleani AND, OR e NOT.
Una "formula booleana quantificata" è una formula booleana che contiene quantificatori universali o esistenziali (o entrambi), ognuno dei quali ha una variabile nel proprio scope.
Una "formula booleana completamente quantificata" è una formula booleana quantificata in cui ogni variabile compare nello scope di un quantificatore.
Una "formula soddisfacibilmente booleana completamente quantificata" non esiste, me la sono inventata ora, ma era divertente continuare ad aggiungere parole.
Il problema TQBF consiste nel determinare se una formula booleana completamente quantificata sia vera. Più formalmente:
TQBF = {Φ | Φ è una formula booleana completamente quantificata vera}
Ed ecco l'agognato teorema da dimostrare:
to:
Per fare l'analisi dell'algoritmo E, consideriamo due casi:
- se (x/2) >= y, dato che (x mod y) < y, avremo che:
(x mod y) < y <= (x/2)
- se (x/2) < y, dato che (x mod y) = x - y, avremo che:
(x mod y) = x - y <= (x/2)
In entrambi i casi avremo che ad ogni passata del ciclo il valore della x viene come minimo dimezzato. Quindi il numero massimo di volte in cui vengono ciclati i passi (2) e (3) di E è il valore più piccolo tra 2logx e 2logy. Essendoci di messo un logaritmo il numero di passi è sicuramente polinomiale, ed essendo ogni operazione di complessità polinomiale il problema RELPRIME è sicuramente in P.
Teorema 3 - sui linguaggi liberi dal contesto
Changed line 136 from:
to:
Ogni linguaggio libero dal contesto è membro di P.
Changed lines 141-142 from:
La prima condizione da verificare è che TQBF sia in PSPACE, cioè se è risolvibile in uno spazio polinomiale con una MdT deterministica. Vediamo se questa va bene:
to:
Sappiamo già dalle lezioni precedenti che i linguaggi liberi dal contesto (da ora CFL) sono decidibili, perché è possibile creare un algoritmo che lo decida. Dobbiamo quindi dimostrare che tale algoritmo viene eseguito in tempo polinomiale. Dov'è la fregatura? Che la dimostrazione della decidibilità di un CFL L tirava in ballo il fatto che era stato generato da una grammatica libera dal contesto G espressa nella forma normale Chomsky, e che bisognava verificare tutte le derivazioni di G per vedere se una certa stringa di L poteva essere accettata. Il numero di derivazioni è ahinoi esponenziale, quindi dobbiamo scegliere un'altra strada per dimostrare il nostro teorema.
Chi di noi non stava pensando alla programmazione dinamica come soluzione? Esatto.
Nella programmazione dinamica si cercano e si utilizzano le soluzioni di sottoproblemi per risolvere il problema principale. Nel nostro caso i sottoproblemi sono le sottostringhe generate per scomposizione dall'originale stringa w generata da G, e dovremo verificare che ognuna di esse possa essere derivata a partire dalle variabili della grammatica. Per fare ciò costruiremo una tabella n x n, con coordinate i e j. In ogni cella (i,j) con i<=j potrò trovare tutte le variabili che mi permettono di generare la sottostringa wiwi+1...wj; al contrario tutte le celle con i>j saranno inutilizzate. Grazie ai principi della programmazione dinamica useremo via via le soluzioni ottenute per le sottostringhe precedenti. Come? Quando andando avanti con la risoluzione scopro che una data (i,j) potevo generarla utilizzando una sottostringa già risolta, nella cella metto quella sottostringa. Come? Ogni sottostringa di lunghezza k+1 può essere divisa in k modi possibili (ad esempio w1w2w3w4 può essere divisa in: w1|w2w3w4, w1w2|w3w4, w1w2w3|w4). Per riutilizzare le informazioni già messe in tabella basterà cercare nella mia grammatica una regola A->BC dove B mi permette di generare la parte sinistra e C la destra.
Ed ora, vediamo la MdT D che fa tutto questo (con "subs" si intenderà "sottostringa"):
Changed lines 148-151 from:
T = "su ingresso Φ: (dove Φ è una formula booleana completamente quantificata)
- se Φ non ha quantificatori vuol dire che è un'espressione con sole costanti, quindi valuta Φ è ACCETTA se è vera; altrimenti RIFIUTA;
- se Φ è uguale a ∃x φ, chiama ricorsivamente T su φ, prima sostituendo 0 a x e poi sostituendo 1 a x. Se uno dei due risultati è accettato, allora ACCETTA; altrimenti RIFIUTA;
- se Φ è uguale a ∀x φ, chiama ricorsivamente T su φ, prima sostituendo 0 a x e poi sostituendo 1 a x. Se entrambi i risultati sono accettati, allora ACCETTA; altrimenti RIFIUTA."
to:
D = "su ingresso w=w1...wn:
1. se w=ε ed S->ε è una regola, ACCETTA;
2. ripeti da i=1 ad i=n:
3. per ogni variabile A:
4. verifica se A->b è una regola, dove b=wi;
5. se sì, inserisci A nella tabella alle coordinate (i,i);
6. ripeti da l=2 ad l=n: (l è la lunghezza della subs)
7. ripeti da i=1 ad i=n-l+1: (i è la posizione iniziale della subs)
8. sia j=i+l-1; (j è la posizione finale della subs)
9. ripeti da k=i a k=j-1: (k è la posizione della separazione)
10. per ogni regola A->BC:
11. se la cella (i,k) contiene B e la cella (k+1,j) contiene C, allora metti A nella cella (i,j)
12. se S è nella cella (1,n) ACCETTA; altrimenti RIFIUTA."
Changed lines 163-294 from:
L'algoritmo T decide TQBF ed usa uno spazio polinomiale, perché è lineare al numero m di variabili di Φ date in ingresso (spazio usato: O(m)).
La seconda condizione da verificare è che qualunque problema A in PSPACE può essere ridotto in tempo polinomiale a TQBF. In altre parole, dato un linguaggio A deciso da una MdT M deterministica (tempo esponenziale) in spazio polinomiale, dobbiamo verificare se è possibile mappare una stringa w in una formula booleana completamente quantificata Φ che sia vera se e solo se M accetta w. Non avete anche voi una sorta di deja-vu? Quello che abbiamo appena detto non ha vaghe somiglianze col problema di Cook-Levin (SAT è NP-completo)? Essì, qualcosa in comune c'è, vediamo dove ci porta questa strada. Dobbiamo costruire una formula Φ che simuli M su un ingresso w esprimendo i requisiti che dovrebbe avere un tableau accettante. Abbiamo un problema però: in Cook-Levin il tableau è nk x nk, mentre in questo caso avremmo larghezza nk (lo spazio usato da M) ma altezza esponenziale dato che M può essere eseguito in tempo esponenziale. Merda: per rappresentare un tableau di dimensione esponenziale dovremo usare una formula di dimensione altrettanto esponenziale, esattamente il risultato che non vogliamo ottenere da una riduzione tempo polinomiale.
Ci viene in aiuto il teorema di Savitch, grazie al quale possiamo dimezzare ad ogni iterazione lo spazio entro cui cercare la soluzione. Riusciamo così a compattare la dimensione esponenziale (che otterremmo applicando paro-paro Cook-Levin) in una polinomiale. La formula di compattamento è questa:
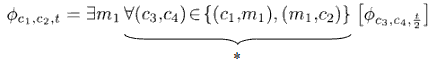 Dove, per qualsiasi coppia (c3,c4), * può essere uguale sia a (c1,m1) che a (m1,c2), quindi sto considerando contemporaneamente la metà superiore e quella inferiore della formula.
Alla prof non interessa che si dimostri (o capisca) come si è arrivati a questa formula, l'importante è credere che sia giusta. Per quanto riguarda la complessità, si tratta di una formula ricorsiva in cui:
- lo spazio usato da ogni ricorsione è lineare alla dimensione della configurazione, quindi è O(f(n));
- il numero di ricorsioni è pari a log(2d*f(n)), quindi O(f(n)).
Ne deriva che la complessità della formula è O(f2(n)), che è polinomiale e quindi soddisfa la seconda condizione da verificare.
Il teorema è dunque dimostrato: TQBF è PSPACE-completo.
Teorema 2 - FORMULA-GAME è PSPACE-completo?
In generale, per gioco si intende una competizione in cui i partecipanti devono raggiungere un certo obiettivo rispettando una serie di regole.
Il FORMULA GAME è un gioco elettrizzante con gli ingredienti giusti per diventare il successo più frizzante dell'estate: quantificatori e valori di verità di formule booleane.
La formula Φ con cui si gioca ha questo aspetto:
Φ = ∃x1 ∀x2 ∃x3 ... Qxk [φ]
, dove Q è un quantificatore universale o esistenziale e φ il resto della formula senza quantificatori (ma con le variabili che si trovano nei loro scope).
Ci sono due giocatori, che giocano a turni alternati:
- giocatore E, che deve dare un valore di verità a tutte le variabili con quantificatore esistenziale. Vince se il valore finale della Φ è pari a 1;
- giocatore A, che deve dare un valore di verità a tutte le variabili con quantificatore universale. Vince se il valore finale della Φ è pari a 0.
Ad esempio, sia data questa formula:
Il giocatore E inizia per primo e dovrà assegnare un valore alla variabile x1. Siccome il suo scopo è fare in modo che la formula risulti pari a 1, per come questa è costruita dovrà riuscire a ottenere un 1 in tutte le sottoformule messe in AND tra loro. Assegnerà x1=1 si assicura un 1 nella prima sottoformula.
Tocca ora ad A, che dovrà intervenire su x2. Il suo scopo è fare in modo che almeno una sottoformula abbia valore 0, così che messa in AND con le altre renda la formula globale pari a 0. Ha senso perciò che assegni x2=0. Si noti però che così facendo ha fatto finire un 1 nella terza sottoformula, in cui era presente la negazione della stessa variabile.
L'ultimo turno spetta ad E, per cui è vita semplice assegnare x3=1 e vincere la partita.
Da tutto questo appare evidente che i giocatori non scelgono a caso i valori, ma adottano una strategia. In particolare diciamo che un giocatore ha una strategia vincente per una partita quando entrambi i contendenti giocano in modo ottimale e riesce comunque a vincere.
Il problema del FORMULA-GAME può essere così definito:
FORMULA-GAME = {φ | il giocatore E ha una strategia vincente nel formula-game associato a φ}
Il teorema da dimostrare è il seguente:
FORMULA-GAME è PSPACE-completo.
Dimostrazione
Invece di dimostrare le due condizioni della PSPACE-completezza possiamo provare a dimostrare che il problema è formulato in modo analogo ad un altro problema PSPACE-completo.
In effetti a pensarci bene FORMULA-GAME è riconducibile a TQBF: la strategia vincente di E è quella che lo porta a rendere la formula pari a 1, esattamente lo stesso scopo di TQFB che vuole che la formula booleana completamente quantificata sia vera. Inoltre in entrambi i casi si interviene sull'assegnamento di valori 0/1 alle variabili, anche se in un caso per vincere e nell'altro per provare la soddisfacibilità.
Poche balle: dato che una formula φ appartiene a TQBF quando φ appartiene a FORMULA-GAME, il teorema è dimostrato dalla stessa dimostrazione di TQBF.
L e NL
Se pensavate che usare spazi lineari poteva soddisfarci vi sbagliavate di grosso. Da questo momento studieremo limiti di spazio sotto-lineari (logaritmici), in cui la macchina legge l'intero ingresso ma non ha spazio sufficiente per memorizzarlo tutto. Va da sé che si tratta di un concetto inapplicabile al tempo, perché significherebbe non avere il tempo di leggere l'intero ingresso.
Per capire meglio la situazione dovremo cambiare modello computazionale: una MdT con due nastri, uno di sola lettura (per gli ingressi) e l'altro di lettura/scrittura (di lavoro). Gli ingressi dovranno rimanere sempre sul primo nastro, mentre sarà quello di lavoro che contruibirà alla spazio complessità della MdT. A queste condizioni possiamo affermare che:
L è la classe di linguaggi che sono decidibili in spazio logaritmico su una MdT deterministica. In altre parole: L=SPACE(logn).
NL è la classe di linguaggi che sono decidibili in spazio logaritmico su una MdT n.d.. In altre parole: NL=NSPACE(logn).
Si noti che il dilemma "L=NL ?" è analogo a quello "P=NP ?".
Esempio L
Come esempio di linguaggio in L consideriamo A={0k1k | k>=0}.
Una MdT che lo descrive potrebbe essere:
M = "su ingresso w: (dove w è una stringa)
1. fai uno scan del nastro e RIFIUTA se c'è uno 0 a destra di un 1;
2. ripeti finché ci sono sia 0 che 1 sul nastro:
3. fai uno scan del nastro, marcando un singolo 0 e un singolo 1;
4. se rimangono degli 0 non marcati mentre tutti gli 1 lo sono (o viceversa),
allora RIFIUTA; altrimenti ACCETTA."
Lo spazio richiesto da M è però lineare al numero di caratteri, quindi non va bene.
Dato però che con una MdT possiamo realizzare qualsiasi funzione eseguibile da un elaboratore, ne potremmo definire una che lavora come contatore. La nostra MdT spazio logaritmica userà allora due contatori, uno per gli 0 e uno per gli 1, e scriverà i risultati sul nastro di lavoro per fare un confronto: se i numeri sono uguali, allora ACCETTA; altrimenti RIFIUTA. Rispetta i requisiti di L? Sì, perché la rappresentazione in binario del numero che quantifica la dimensione di una stringa di caratteri (gli 0 e gli 1) è logaritmica alla dimensione stessa. Sopracciglio alzato? Facciamo un esempio di stringa di 30 caratteri, e subito sotto il numero binario che ne indica la dimensione:
000000000000000000000000000000
11110
Un bel risparmio di spazio, no?!
Quindi A appartiene alla classe L.
Esempio NL
Nel capitolo sulla Complessità nel tempo abbiamo dimostrato che il problema PATH è in P. Ora vogliamo vedere se è anche in NL.
Dato un grafo diretto G, il problema PATH ha come obiettivo quello di determinare se esiste un percorso diretto tra due nodi s e t. Più formalmente:
PATH = {<G,s,t> | G è un grafo diretto che ha percorso diretto tra s e t}
Supponiamo di avere una MdT n.d., e selezioniamo in modo n.d. un nodo collegato ad s, memorizzandolo (solo lui) sul nastro. Ripetiamo l'operazione sull'ultimo nodo selezionato, andando a sovrascrivere l'identificativo del nuovo nodo estratto in modo n.d.. Continuiamo a ciclare finché non si è raggiunto il nodo t, o finché il numero di iterazioni non sia maggiore del numero dei nodi (così da escludere loop infiniti su un percorso).
Questo algoritmo garantisce la soluzione del problema in uno spazio logaritmico, quindi PATH è in NL.
NL-completezza
Dopo NP-completezza e NSPACE-completezza, non potevamo perdere la ghiotta occasione di parlare di NL-completezza.
In generale possiamo dire che un linguaggio è NL-completo se è in NL e se ogni altro linguaggio in NL è riducibile al linguaggio considerato. La riducibilità non può però avvenire in tempo-polinomiale (tutti i problemi sotto-lineari come il nostro sono risolvibili in tempo-polinomiale), ma dobbiamo introdurre un nuovo tipo di riducibilità, quella spazio-logaritmica.
Un trasduttore spazio logaritmico è una MdT con un nastro in sola lettura (ingressi), uno in sola scrittura (uscite) ed uno di lavoro in lettura/scrittura. Il nastro di lavoro può contenere O(logn) simboli. Un trasduttore spazio logaritmico M computa una funzione f:Σ*->Σ*, dove f(w) è la stringa che rimane sul nastro di uscita al termine di M eseguito su ingresso w. Chiamiamo f log space computable function. Il linguaggio A è spazio-logaritmico riducibile a B, scritto A≤LB, se A è mapping riducibile a B utilizzando una log space computable function f.
Ora sì che possiamo definire la NL-completezza:
Un linguaggio B è NL-completo se soddisfa due condizioni:
- B è in NL;
- Ogni A in NL è spazio-logaritmico riducibile a B.
Ciliegina sulla torta, citiamo due teoremi sulla NL-completezza (che non dimostreremo).
Se A≤LB e B appartiene ad L, allora A appartiene ad L.
Il corollario è la solita speranzosa strada da battere per verificare se L=NL:
Se un linguaggio NL-completo è in L, allora L=NL.
Teorema 3 - PATH è NL-completo?
Dimostrazione
La prima condizione da verificare è che PATH sia in NL, e l'abbiamo dimostrato poche righe fa nel paragrafo "Esempio NL".
La seconda condizione da verificare è che ogni A in NL è spazio-logaritmico riducibile a PATH. In altre parole, dato un linguaggio A deciso da una MdT M in spazio logaritmico, dobbiamo verificare se è possibile mappare una stringa w in un grafo G che abbia un percorso diretto tra s e t se e solo se M accetta w.
L'idea dietro la riduzione spazio logaritmica da A a PATH è quella di costruire un grafo che rappresenti la computazione della MdT n.d. spazio logaritmica che risolve A. Basterà dunque far corrispondere ad ogni configurazione di M un nodo del grafo, ed unirne due con un arco se e solo se esiste una transizione possibile (permessa dalle funzioni di transizione del linguaggio) che giustifichi il passaggio da una configurazione all'altra. In tutto questo avremo premura di far corrispondere al nodo s la configurazione iniziale di M, e a t quella terminale accettata.
Ora che sappiamo come ridurre, dobbiamo dimostrare che riusciamo a farlo utilizzando un trasduttore spazio logaritmico; nel nastro in sola lettura ci mettiamo l'ingresso w, e su quello di uscita la descrizione di G, composta da una lista di nodi e una lista di archi. Per verificare se si può passare da una configurazione all'altra (quindi il controllo degli archi) posso memorizzare solo le celle intorno la testina, perché sono le uniche che cambieranno (dunque le uniche con informazioni utili). In questo modo si riesce ad utilizzare uno spazio logaritmico rispetto alla dimensione dell'ingresso w, dimostrando perciò la seconda condizione.
Poiché entrambe le condizioni sono state dimostrate, possiamo affermare che PATH è NL-completo.
to:
In altre parole, se nell'ultima colonna della prima riga ci ritroviamo la variabile iniziale S l'algoritmo ha successo. Via quelle sopracciglia alzate, facciamo piuttosto l'analisi dell'algoritmo considerando i passaggi più critici:
- (4) e (5) possono essere ripetuti al più n*v volte, dove v è il numero di variabili della grammatica. Dato che v è comunque una costante (non dipende dalla n), entrambi i passi hanno complessità O(n);
- (6) può essere svolto al più n volte, quindi è O(n);
- (7) viene ripetuto al più n volte tutte le volte che viene eseguito (6), quindi avrà complessità O(n)*n =O(n2);
- (8) e (9) vengono ripetuti al più n volte tutte le volte che viene eseguito (7), quindi avranno complessità O(n2)*n =O(n3);
- (10) e quindi (11) vengono eseguiti ogni volta che partono (8) e (9), e vengono ripetuti r volte, dove r è il numero di regole. Avranno quindi complessità O(n3)*r=O(n3) (perché r è costante).
La complessità totale dell'algoritmo sarà dunque O(n)+O(n3)=O(n3), che è meravigliosamente polinomiale. Quindi abbiamo dimostrato che ogni linguaggio libero dal contesto è in P.
Changed lines 114-115 from:
Perché per parliamo di tempo riducibilità e non di spazio riducibilità? Ma per non complicarci troppo la vita, belin! Life is too short! (i problemi completi sono i più difficili di tutti, ed una volta che abbiamo verificato che è in PSPACE chi se ne frega se consideriamo la riducibilità nel tempo o nello spazio)
to:
Perché parliamo di tempo riducibilità e non di spazio riducibilità? Ma per non complicarci troppo la vita, belin! Life is too short! (i problemi completi sono i più difficili di tutti, ed una volta che abbiamo verificato che è in PSPACE chi se ne frega se consideriamo la riducibilità nel tempo o nello spazio)
Changed lines 234-239 from:
to:
Dopo NP-completezza e NSPACE-completezza, non potevamo perdere la ghiotta occasione di parlare di NL-completezza.
In generale possiamo dire che un linguaggio è NL-completo se è in NL e se ogni altro linguaggio in NL è riducibile al linguaggio considerato. La riducibilità non può però avvenire in tempo-polinomiale (tutti i problemi sotto-lineari come il nostro sono risolvibili in tempo-polinomiale), ma dobbiamo introdurre un nuovo tipo di riducibilità, quella spazio-logaritmica.
Un trasduttore spazio logaritmico è una MdT con un nastro in sola lettura (ingressi), uno in sola scrittura (uscite) ed uno di lavoro in lettura/scrittura. Il nastro di lavoro può contenere O(logn) simboli. Un trasduttore spazio logaritmico M computa una funzione f:Σ*->Σ*, dove f(w) è la stringa che rimane sul nastro di uscita al termine di M eseguito su ingresso w. Chiamiamo f log space computable function. Il linguaggio A è spazio-logaritmico riducibile a B, scritto A≤LB, se A è mapping riducibile a B utilizzando una log space computable function f.
Ora sì che possiamo definire la NL-completezza:
Un linguaggio B è NL-completo se soddisfa due condizioni:
- B è in NL;
- Ogni A in NL è spazio-logaritmico riducibile a B.
Ciliegina sulla torta, citiamo due teoremi sulla NL-completezza (che non dimostreremo).
Se A≤LB e B appartiene ad L, allora A appartiene ad L.
Il corollario è la solita speranzosa strada da battere per verificare se L=NL:
Se un linguaggio NL-completo è in L, allora L=NL.
Teorema 3 - PATH è NL-completo?
Dimostrazione
La prima condizione da verificare è che PATH sia in NL, e l'abbiamo dimostrato poche righe fa nel paragrafo "Esempio NL".
La seconda condizione da verificare è che ogni A in NL è spazio-logaritmico riducibile a PATH. In altre parole, dato un linguaggio A deciso da una MdT M in spazio logaritmico, dobbiamo verificare se è possibile mappare una stringa w in un grafo G che abbia un percorso diretto tra s e t se e solo se M accetta w.
L'idea dietro la riduzione spazio logaritmica da A a PATH è quella di costruire un grafo che rappresenti la computazione della MdT n.d. spazio logaritmica che risolve A. Basterà dunque far corrispondere ad ogni configurazione di M un nodo del grafo, ed unirne due con un arco se e solo se esiste una transizione possibile (permessa dalle funzioni di transizione del linguaggio) che giustifichi il passaggio da una configurazione all'altra. In tutto questo avremo premura di far corrispondere al nodo s la configurazione iniziale di M, e a t quella terminale accettata.
Ora che sappiamo come ridurre, dobbiamo dimostrare che riusciamo a farlo utilizzando un trasduttore spazio logaritmico; nel nastro in sola lettura ci mettiamo l'ingresso w, e su quello di uscita la descrizione di G, composta da una lista di nodi e una lista di archi. Per verificare se si può passare da una configurazione all'altra (quindi il controllo degli archi) posso memorizzare solo le celle intorno la testina, perché sono le uniche che cambieranno (dunque le uniche con informazioni utili). In questo modo si riesce ad utilizzare uno spazio logaritmico rispetto alla dimensione dell'ingresso w, dimostrando perciò la seconda condizione.
Poiché entrambe le condizioni sono state dimostrate, possiamo affermare che PATH è NL-completo.
Changed line 1 from:
(:title Informatica Teorica - Complessità nel tempo:)
to:
(:title Informatica Teorica - Spazio-complessità:)
Changed lines 5-25 from:
:: Informatica Teorica - Complessità nel tempo ::
Appunti & Dimostrazioni del 5 Maggio
Cenni teorici
Sia M una Macchina di Touring (da ora MdT) deterministica che si ferma su ogni ingresso. Il tempo di esecuzione o complessità nel tempo di M è la funzione f: N -> N, dove f(n) è il numero massimo di passi che M impiega su ogni ingresso di lunghezza n. Se f(n) è il tempo di esecuzione di M, diciamo che M è eseguita in tempo f(n) e che M è una tempo f(n) MdT.
Della complessità nel tempo non si dà una misura precisa, ma una stima risultante dall'analisi asintotica dell'algoritmo. In particolare introduciamo le notazioni O ("o grande") e o ("o piccolo").
Siano f e g due funzioni f,g: N -> R+. Diciamo che f(n) = O(g(n)) se esistono due interi positivi c e n0 tali che per ogni intero n>=n0:
f(n) >= c*g(n)
Quando f(n) = O(g(n)) diciamo che g(n) è un limite superiore (upper bound) per f(n), o più precisamente che g(n) è un limite superiore asintotico per f(n), per enfatizzare il fatto che stiamo ignorando le costanti.
Se O può essere definita come una funzione asintoticamente "non maggiore" di un'altra (minore o uguale), con o piccolo definiamo una funzione asintoticamente "minore" di un'altra (strettamente minore). Facendo qualche esempio:
- n = o(nlog(logn))
- nlog(logn) = o(n(logn))
- n2 = o(n3)
Perché abbiamo parlato di o grandi e o piccole? Perché quando si fa l'analisi asintotica di un algoritmo si considerano solo i termini di ordine maggiore che partecipano a formare il tempo di esecuzione complessivo, trascurando i coefficienti, le costanti e tutti i termini di grado inferiore.
Ad esempio: f(n) = 3n3 + 2n2 + n + 100 = O(n3)
Concludiamo definendo cos'è una classe di complessità nel tempo:
to:
:: Informatica Teorica - Spazio-complessità ::
Appunti & Dimostrazioni del 19 Maggio
Complessità in termini di spazio
Così come è possibile quantificare la complessità di un algoritmo in funzione della risorsa tempo, si può fare lo stesso considerando la risorsa spazio, ovvero la memoria utilizzata. Per misurarla si utilizzerà una MdT M, e in particolare:
- se M è
deterministica, allora la sua spazio complessità è la funzione f(n), cioè il massimo numero di celle del nastro su cui M farà uno scan per ogni ingresso di lunghezza n;
- se M è
non deterministica (da ora, n.d.), allora la sua spazio complessità f(n) sarà il numero massimo di celle del nastro su cui M farà uno scan per ogni ramo della sua computazione e per ogni ingresso di lunghezza n.
Quella che ci interessa è però la stima asintotica della spazio-complessità, che può essere così definita:
Changed lines 17-19 from:
Sia t:N->R+ una a funzione. Definiamo la classe di complessità nel tempo, TIME(t(n)), come l'insieme di tutti i linguaggi che sono decidibili in tempo O(t(n)) (polinomiale) da una MdT.
to:
Sia f:N->R+ una funzione. Le classi di spazio complessità, SPACE(f(n)) ed NSPACE(f(n)), sono definite come segue:
- SPACE(f(n)) = {L|L è un linguaggio deciso da una MdT deterministica O(f(n))-spazio}
- NSPACE(f(n)) = {L|L è un linguaggio deciso da una MdT
n.d. O(f(n))-spazio}
Changed lines 22-25 from:
Teorema 1 - sulle relazioni di complessità tra modelli
Sia t(n) una funzione, con t(n)>=n. Ogni MdT multinastro t(n)-tempo ha una equivalente MdT a nastro singolo O(t2(n))-tempo.
to:
Esempio 1: SAT è spazio-lineare?
Sappiamo che il problema SAT è NP-completo, e che quindi non può essere risolto con una MdT deterministica in tempo polinomiale. Figurarsi se ci riesce in tempo lineare. Lo spazio ha però una caratteristica in più rispetto al tempo: può essere riutilizzato!
L'idea per la nostra MdT che risolve il problema SAT in spazio lineare, è quella di assegnare una cella ad ogni variabile, e riutilizzarla ogni volta che facciamo un nuovo assegnamento:
M = "su ingresso Φ: (dove Φ è una formula booleana)
1. per ogni valore di verità assegnato alle variabili x 1..x n di Φ:
2. valuta Φ sull'assegnamento;
3. se Φ=1 in almeno un assegnamento, allora ACCETTA; altrimenti RIFIUTA."
Added lines 33-60:
M è evidentemente spazio-lineare, perché ad ogni iterazione utilizza sempre lo stesso spazio in memoria, lineare al numero di variabili. Dato che tale numero è al più pari ad n, la lunghezza dell'ingresso, allora possiamo dire che la macchina è eseguita in O(n)-spazio.
Esempio 2: (not)ALL è spazio-lineare?
Consideriamo ora un problema risolvibile con una MdT n.d., il problema ALLNFA, che deve stabilire se un determinato linguaggio accetta tutte le stringhe. Più formalmente:
ALLNFA = {<A> | A è un NFA ed L(A)=Σ*}
A noi non interessa il problema ALLNFA, ma il suo complementare, di cui vogliamo trovare una MdT n.d. spazio-lineare che lo risolva. L'idea è quella di usare il non determinismo per trovare una stringa che sia rifiutata dall'NFA, ed usare uno spazio lineare per tenere traccia degli stati in cui l'automa può trovarsi in un determinato momento. Lineare a cosa? Semplice: al numero q di stati in cui può trovarsi l'NFA, di cui ricordiamo possono esserne contemporaneamente attivi 2q, ognuno rappresentato con un simbolo.
Scriviamo la MdT N:
N = "su ingresso <M>: (dove <M> è un NFA)
1. metti un marker sullo stato iniziale dell'NFA;
2. ripeti 2 q volte:
3. seleziona in modo n.d. un simbolo d'ingresso e aggiorna le posizioni dei marker sugli stati di M;
4. se nessun marker è su uno stato accettante, allora ACCETTA; altrimenti RIFIUTA."
Si noti che il passo 3 non fa altro che simulare la lettura del simbolo selezionato in modo n.d..
Per come è stato costruito N, l'unico spazio di cui ha bisogno è quello per memorizzare le posizioni dei marker e per il contatore del ciclo descritto ai passi (2) e (3). Si tratta quindi di uno spazio lineare all'ingresso, perché ad ogni iterazione andrò a scrivere sempre sulle stesse celle di memoria!
Teorema di Savitch
La MdT deterministica che simula la corrispondente n.d. ha una complessità tempo esponenziale rispetto al suo modello. Il teorema di Savitch dimostra invece che nello spazio la complessità non aumenta allo stesso modo, ma molto meno.
Per ogni funzione f:N->R+, dove f(n)>=n,
Changed lines 63-73 from:
Consideriamo M una MdT con k nastri, ed S la corrispondente MdT a nastro singolo. S è costruita copiando i contenuti dei k nastri sul suo mettendoli in fila uno dopo l'altro e separandoli con un #. Perché S riesca a simulare un singolo passo di M su un certo nastro, dovrà prima posizionare la propria testina sul punto corrispondente, e solo dopo compiere l'operazione. Sappiamo dal testo del teorema che nel peggiore dei casi la testina di M impiegherà t(n) tempo per raggiungere il punto desiderato e compiere l'operazione, quindi avrà complessità O(t(n)). La complessità di S sarà dunque data dai contributi derivanti dalle seguenti operazioni:
- ricopiare correttamente il contenuto di M, impiegando O(n) passi
- simulare M su nastro singolo, impiegando t(n) passaggi ognuno con complessità O(t(n)). Ovvero: t(n)*O(t(n))=O(t2(n))
Dato che tra O(n) e O(t2(n)) il secondo è il contributo più importante, trascuriamo il primo è affermiamo che simulare una multinastro su MdT a nastro singolo richiede il quadrato del tempo di esecuzione.
Teorema 2 - sulle relazioni di complessità tra modelli
Sia t(n) una funzione, con t(n)>=2. Ogni MdT a singolo nastro non-deterministica t(n)-tempo ha una equivalente MdT a nastro singolo deterministica 2O(t(n))-tempo.
to:
La situazione: partiamo con una MdT n.d. f(n)-spazio, e dobbiamo simularla in modo deterministico sapendo che con quella si potranno avere più scelte per ogni nodo.
Una prima idea è simulare tutti i possibili rami della n.d., ma così facendo non potremo sovrascrivere l'area di memoria utilizzata, perché dobbiamo tenere traccia di quale ramo termina e quale no; con questa strategia si userebbe quindi uno spazio esponenziale, e non va bene.
La soluzione è introdurre un nuovo problema, quello che ci permette di verificare se una MdT n.d. può passare da una configurazione iniziale c1 a quella finale c2 in un numero di passi minore o uguale a t. Chiamiamo questo secondo problema yieldability problem, e lo risolviamo definendo la MdT deterministica e ricorsiva CANYIELD.
Arriviamo al dunque.
Data una MdT n.d. N che decide un linguaggio A in uno spazio f(n), costruiamo la MdT deterministica M che utilizzando la procedura CANYIELD riesce a decidere A. N avrà come input la stringa w da verificare, mentre CANYIELD riceverà in ingresso le due configurazioni c1 e c2 , ed il numero massimo di passi impiegabili t.
CANYIELD = "su ingresso c1, c2, t:
- se t=1, verifica se c1=c2 o se c1->c2 in un unico passo in accordo alle regole di N. Se uno dei due test va a buon fine, ACCETTA; altrimenti RIFIUTA;
2. se t>1, per ogni configurazione c m di N su w che usa spazio f(n);
3. esegui CANYIELD su ingresso c1, cm, t/2;
4. esegui CANYIELD su ingresso cm, c2, t/2;
5. se (3) e (4) vanno entrambi a buon fine, allora ACCETTA; altrimenti RIFIUTA."
Changed lines 79-106 from:
Dimostrazione
Data una MdT non deterministica N con tempo di esecuzione t(n), sappiamo che è possibile creare una MdT deterministica D equivalente che intraprende ogni possibile ramo della computazione non deterministica. In particolare, dato un ingresso di lunghezza n (la grandezza della stringa w) ogni ramo dell'albero di computazione non deterministica di N avrà al massimo lunghezza t(n). Supponendo che ogni nodo possa avere al massimo b figli (ovvero le scelte legali della funzione di transizione), avremo al massimo bt(n) foglie.
Per rendere più efficiente l'algoritmo, l'esplorazione dell'albero alla ricerca dello stato di accettazione non viene fatta in profondità (dalla radice alla foglia e poi da capo con un altro percorso), ma in ampiezza (controllando gli stati dei nodi livello per livello).
Il numero di nodi nell'albero è di poco inferiore al doppio delle foglie, quindi possiamo dare come limite superiore al numero di nodi O(bt(n)). A questo punto, sapendo che il tempo di esplorazione dalla radice a qualunque nodo è pari a O(t(n)), e che nel caso peggiore bisognerà visitare tutti gli O(bt(n)) nodi dell'albero, il tempo totale di esecuzione dell'algoritmo D è pari a:
O(t(n)*bt(n)) = 2O(t(n))
Facciamo qualche considerazione conclusiva sull'equivalenza O(t(n)*bt(n))=2O(t(n)):
- si tratta di un prodotto tra un polinomio e un'esponenziale, ed avendo quest'ultimo un ordine di grandezza maggiore, è possibile trascurare il primo e considerare come complessità dell'algoritmo solo O(bt(n))
- per una serie di motivi che non ci interessano (che riguardano comunque la teoria della complessità), è possibile passare da O(bt(n)) a O(2t(n))
- siccome la base 2 è una costante, possiamo portare in alto l'o grande: O(2t(n))=2O(t(n))
Il teorema sembra già dimostrato, ma in realtà non va dimenticato che la D che simula N non è più una MdT a singolo nastro, ma per costruzione ne ha 3. Poco male: dal Teorema 1 sopra riportato sappiamo che ogni MdT multinastro t(n)-tempo ha una equivalente MdT a nastro singolo O(t2(n))-tempo. Quindi:
(2O(t(n)))2 = 2O(2t(n)) = 2O(t(n))
Dimostrazione conclusa.
Classe P
Introduciamo ora la classe P, ovvero la classe dei linguaggi che sono decidibili in tempo polinomiale su una MdT deterministica a singolo nastro. Si tratta di una classe matematicamente robusta, che non dipende quindi dal modello computazionale che sceglieremo per risolvere il problema.
I problemi in P, o tempo-polinomiali, sono una classe di problemi realisticamente risolvibili con un calcolatore. Per dimostrare che un problema è tempo-polinomiale bisognerà prima dare un limite polinomiale superiore (in notazione O grande) per il numero di passi che l'algoritmo usa per un ingresso di lunghezza n, poi esaminare ogni passo della descrizione dell'algoritmo per assicurarci che ogni passo sia tempo-polinomiale.
PATH è P?
Dato un grafo diretto G, il problema PATH ha come obiettivo quello di determinare se esiste un percorso diretto tra due nodi s e t. Più formalmente:
PATH = {<G,s,t> | G è un grafo diretto che ha percorso diretto tra s e t}
Per dimostrare che PATH appartiene a P dovremo dimostrare che è risolvibile in tempo polinomiale. Una possibile strada è quella di partire da s e marcare tutti i nodi raggiungibili con passo 1, quindi ripetere l'operazione a partire da essi (raggiungendo una distanza da s pari a 2). L'operazione va ripetuta finché non è più possibile marcare nuovi nodi. A questo punto bisogna verificare se t è stato segnato o no: se sì PATH è vero, altrimenti no.
Costruiamo ora la MdT deterministica M che implementa l'algoritmo:
to:
Passiamo ora a definire la MdT M che simula N, e per farlo introduciamo alcuni accorgimenti:
- quando N accetta pulisce l'intero contenuto del nastro e lo sostituisce con la configurazione caccept;
- chiamiamo cstart la configurazione iniziale di N sulla stringa d'ingresso w;
- selezioniamo una costante d tale che N non abbia un numero di configurazioni maggiore di 2d*f(n), dove n è la lunghezza di w. In questo modo fissiamo un limite superiore al tempo di computazione per ogni ramo, e creiamo un legame tra numero di configurazioni possibili e tempo.
Changed lines 85-89 from:
M = "su ingresso <G,s,t>:
1. marca s;
2. ripeti finché non abbiamo nuovi nodi da marcare:
3.fai una scan degli archi di G. Se trovi l'arco (a,b), dove a è un nodo marcato e b no, marca b;
4. se t è marcato, allora ACCETTA; altrimenti RIFIUTA."
to:
M = "su ingresso w:
- restituisci il risultato di CANYIELD(cstart, caccept,2d*f(n))."
Changed lines 89-106 from:
Facciamo l'analisi dell'algoritmo:
- i passi (1) e (4) sono ripetuti una sola volta
- i passi (2) e (3) (il loop) sono eseguiti m volte, dove m è il numero di nodi
Quindi, dato che il numero di passi è 1+1+m e che ognuno di essi ha complessità polinomiale, PATH è in P.
RELPRIME è P?
Prima di tutto, di cosa diavolo stiamo parlando? Il problema RELPRIME è quello che deve verificare se due numeri sono primi tra loro, ovvero se il più grande intero che li divide entrambi è 1. Più formalmente:
RELPRIME = {<x,y> | x e y sono primi tra loro}
Per dimostrare che RELPRIME appartiene a P dobbiamo trovare una MdT deterministica che lo risolva in tempo polinomiale. Iniziamo a scrivere una MdT che calcoli il divisore maggiore dati due interi x e y:
E = "su ingresso <x,y>:
1. ripeti finché y=0;
2. assegna a x il valore x mod y;
3. scambia x e y;
4. output: x"
to:
Dato che CANYIELD risolve sicuramente l'yieldability problem, possiamo affermare che M simula correttamente N. Non ci resta che fare l'analisi dell'algoritmo, e verificare se M è eseguito in O(f2(n)) spazio, come sostiene il teorema. Cosa dobbiamo fare? Calcolare quanto spazio richiede ogni ricorsione di CANYIELD e moltiplicarlo per il numero di ricorsioni stesse.
Ogni volta che CANYIELD invoca sé stesso ricorsivamente, memorizza il numero di stato corrente e i valori di c1 c2 e t su uno stack, così che possano essere ripristinati una volta tornati dalla chiamata ricorsiva. Ogni livello di ricorsione richiede quindi uno spazio addizionale O(f(n)).
Considerato che ad ogni ricorsione dimezziamo il numero di passi impiegabili t, e che inizialmente t è pari a 2d*f(n), il numero di ricorsioni è:
O(log2d*f(n)) = O(d*f(n)) = O(f(n))
Quindi, spazio richiesto ad ogni ricorsione per il numero di ricorsioni:
O(f(n)) * O(f(n)) = O(f2(n)), come sostenuto dal teorema di Savitch.
Classe PSPACE e PSPACE-completezza
PSPACE è la classe di linguaggi decidibili in spazio polinomiale usando una MdT deterministica. In altre parole:
Changed lines 103-118 from:
Facciamo un esempio di risoluzione. Dati in ingresso x=24 e y=18:
(1)
(2) x = 24 mod 18 = 6
(3) x = 18 , y = 6
(1) y=0? NO
(2) x = 18 mod 6 = 0
(3) x = 6 , y = 0
(1) y=0? SÌ
(4) output: 6
Creiamo ora una seconda MdT che usa E come subroutine:
R = "su ingresso <x,y>:
- esegui E su ingresso <x,y>;
- se il risultato è 1, allora ACCETTA; altrimenti RIFIUTA."
to:
Analogamente, NPSPACE sarà la classe di linguaggi decidibili in spazio polinomiale usando una MdT n.d.. Si noti che per il teorema di Savitch è possibile simulare una MdT deterministica spazio-polinomiale con una MdT n.d. anch'essa spazio-polinomiale. Quindi possiamo affermare che NPSPACE=PSPACE, al contrario di quanto avviene per la tempo-complessità.
Per quanto riguarda la completezza, possiamo affermare che:
Un linguaggio B è PSPACE-completo se soddisfa due condizioni:
- B è in PSPACE;
- Ogni A in PSPACE è riducibile in tempo polinomiale a B.
Se B soddisfa solo la seconda condizione è chiamato PSPACE-hard.
Changed lines 114-123 from:
Per fare l'analisi dell'algoritmo E, consideriamo due casi:
- se (x/2) >= y, dato che (x mod y) < y, avremo che:
(x mod y) < y <= (x/2)
- se (x/2) < y, dato che (x mod y) = x - y, avremo che:
(x mod y) = x - y <= (x/2)
In entrambi i casi avremo che ad ogni passata del ciclo il valore della x viene come minimo dimezzato. Quindi il numero massimo di volte in cui vengono ciclati i passi (2) e (3) di E è il valore più piccolo tra 2logx e 2logy. Essendoci di messo un logaritmo il numero di passi è sicuramente polinomiale, ed essendo ogni operazione di complessità polinomiale il problema RELPRIME è sicuramente in P.
Teorema 3 - sui linguaggi liberi dal contesto
to:
Perché per parliamo di tempo riducibilità e non di spazio riducibilità? Ma per non complicarci troppo la vita, belin! Life is too short! (i problemi completi sono i più difficili di tutti, ed una volta che abbiamo verificato che è in PSPACE chi se ne frega se consideriamo la riducibilità nel tempo o nello spazio)
Teorema 1 - TQBF è PSPACE-completo?
Una "formula booleana" è un'espressione che contiene variabili booleane, costanti 0 e 1, e gli operatori booleani AND, OR e NOT.
Una "formula booleana quantificata" è una formula booleana che contiene quantificatori universali o esistenziali (o entrambi), ognuno dei quali ha una variabile nel proprio scope.
Una "formula booleana completamente quantificata" è una formula booleana quantificata in cui ogni variabile compare nello scope di un quantificatore.
Una "formula soddisfacibilmente booleana completamente quantificata" non esiste, me la sono inventata ora, ma era divertente continuare ad aggiungere parole.
Il problema TQBF consiste nel determinare se una formula booleana completamente quantificata sia vera. Più formalmente:
TQBF = {Φ | Φ è una formula booleana completamente quantificata vera}
Ed ecco l'agognato teorema da dimostrare:
Changed line 128 from:
Ogni linguaggio libero dal contesto è membro di P.
to:
Changed lines 133-138 from:
Sappiamo già dalle lezioni precedenti che i linguaggi liberi dal contesto (da ora CFL) sono decidibili, perché è possibile creare un algoritmo che lo decida. Dobbiamo quindi dimostrare che tale algoritmo viene eseguito in tempo polinomiale. Dov'è la fregatura? Che la dimostrazione della decidibilità di un CFL L tirava in ballo il fatto che era stato generato da una grammatica libera dal contesto G espressa nella forma normale Chomsky, e che bisognava verificare tutte le derivazioni di G per vedere se una certa stringa di L poteva essere accettata. Il numero di derivazioni è ahinoi esponenziale, quindi dobbiamo scegliere un'altra strada per dimostrare il nostro teorema.
Chi di noi non stava pensando alla programmazione dinamica come soluzione? Esatto.
Nella programmazione dinamica si cercano e si utilizzano le soluzioni di sottoproblemi per risolvere il problema principale. Nel nostro caso i sottoproblemi sono le sottostringhe generate per scomposizione dall'originale stringa w generata da G, e dovremo verificare che ognuna di esse possa essere derivata a partire dalle variabili della grammatica. Per fare ciò costruiremo una tabella n x n, con coordinate i e j. In ogni cella (i,j) con i<=j potrò trovare tutte le variabili che mi permettono di generare la sottostringa wiwi+1...wj; al contrario tutte le celle con i>j saranno inutilizzate. Grazie ai principi della programmazione dinamica useremo via via le soluzioni ottenute per le sottostringhe precedenti. Come? Quando andando avanti con la risoluzione scopro che una data (i,j) potevo generarla utilizzando una sottostringa già risolta, nella cella metto quella sottostringa. Come? Ogni sottostringa di lunghezza k+1 può essere divisa in k modi possibili (ad esempio w1w2w3w4 può essere divisa in: w1|w2w3w4, w1w2|w3w4, w1w2w3|w4). Per riutilizzare le informazioni già messe in tabella basterà cercare nella mia grammatica una regola A->BC dove B mi permette di generare la parte sinistra e C la destra.
Ed ora, vediamo la MdT D che fa tutto questo (con "subs" si intenderà "sottostringa"):
to:
La prima condizione da verificare è che TQBF sia in PSPACE, cioè se è risolvibile in uno spazio polinomiale con una MdT deterministica. Vediamo se questa va bene:
Changed lines 136-148 from:
D = "su ingresso w=w1...wn:
1. se w=ε ed S->ε è una regola, ACCETTA;
2. ripeti da i=1 ad i=n:
3. per ogni variabile A:
4. verifica se A->b è una regola, dove b=wi;
5. se sì, inserisci A nella tabella alle coordinate (i,i);
6. ripeti da l=2 ad l=n: (l è la lunghezza della subs)
7. ripeti da i=1 ad i=n-l+1: (i è la posizione iniziale della subs)
8. sia j=i+l-1; (j è la posizione finale della subs)
9. ripeti da k=i a k=j-1: (k è la posizione della separazione)
10. per ogni regola A->BC:
11. se la cella (i,k) contiene B e la cella (k+1,j) contiene C, allora metti A nella cella (i,j)
12. se S è nella cella (1,n) ACCETTA; altrimenti RIFIUTA."
to:
T = "su ingresso Φ: (dove Φ è una formula booleana completamente quantificata)
- se Φ non ha quantificatori vuol dire che è un'espressione con sole costanti, quindi valuta Φ è ACCETTA se è vera; altrimenti RIFIUTA;
- se Φ è uguale a ∃x φ, chiama ricorsivamente T su φ, prima sostituendo 0 a x e poi sostituendo 1 a x. Se uno dei due risultati è accettato, allora ACCETTA; altrimenti RIFIUTA;
- se Φ è uguale a ∀x φ, chiama ricorsivamente T su φ, prima sostituendo 0 a x e poi sostituendo 1 a x. Se entrambi i risultati sono accettati, allora ACCETTA; altrimenti RIFIUTA."
Changed lines 142-149 from:
In altre parole, se nell'ultima colonna della prima riga ci ritroviamo la variabile iniziale S l'algoritmo ha successo. Via quelle sopracciglia alzate, facciamo piuttosto l'analisi dell'algoritmo considerando i passaggi più critici:
- (4) e (5) possono essere ripetuti al più n*v volte, dove v è il numero di variabili della grammatica. Dato che v è comunque una costante (non dipende dalla n), entrambi i passi hanno complessità O(n);
- (6) può essere svolto al più n volte, quindi è O(n);
- (7) viene ripetuto al più n volte tutte le volte che viene eseguito (6), quindi avrà complessità O(n)*n =O(n2);
- (8) e (9) vengono ripetuti al più n volte tutte le volte che viene eseguito (7), quindi avranno complessità O(n2)*n =O(n3);
- (10) e quindi (11) vengono eseguiti ogni volta che partono (8) e (9), e vengono ripetuti r volte, dove r è il numero di regole. Avranno quindi complessità O(n3)*r=O(n3) (perché r è costante).
La complessità totale dell'algoritmo sarà dunque O(n)+O(n3)=O(n3), che è meravigliosamente polinomiale. Quindi abbiamo dimostrato che ogni linguaggio libero dal contesto è in P.
to:
L'algoritmo T decide TQBF ed usa uno spazio polinomiale, perché è lineare al numero m di variabili di Φ date in ingresso (spazio usato: O(m)).
La seconda condizione da verificare è che qualunque problema A in PSPACE può essere ridotto in tempo polinomiale a TQBF. In altre parole, dato un linguaggio A deciso da una MdT M deterministica (tempo esponenziale) in spazio polinomiale, dobbiamo verificare se è possibile mappare una stringa w in una formula booleana completamente quantificata Φ che sia vera se e solo se M accetta w. Non avete anche voi una sorta di deja-vu? Quello che abbiamo appena detto non ha vaghe somiglianze col problema di Cook-Levin (SAT è NP-completo)? Essì, qualcosa in comune c'è, vediamo dove ci porta questa strada. Dobbiamo costruire una formula Φ che simuli M su un ingresso w esprimendo i requisiti che dovrebbe avere un tableau accettante. Abbiamo un problema però: in Cook-Levin il tableau è nk x nk, mentre in questo caso avremmo larghezza nk (lo spazio usato da M) ma altezza esponenziale dato che M può essere eseguito in tempo esponenziale. Merda: per rappresentare un tableau di dimensione esponenziale dovremo usare una formula di dimensione altrettanto esponenziale, esattamente il risultato che non vogliamo ottenere da una riduzione tempo polinomiale.
Ci viene in aiuto il teorema di Savitch, grazie al quale possiamo dimezzare ad ogni iterazione lo spazio entro cui cercare la soluzione. Riusciamo così a compattare la dimensione esponenziale (che otterremmo applicando paro-paro Cook-Levin) in una polinomiale. La formula di compattamento è questa:
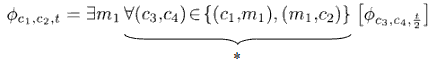 Dove, per qualsiasi coppia (c3,c4), * può essere uguale sia a (c1,m1) che a (m1,c2), quindi sto considerando contemporaneamente la metà superiore e quella inferiore della formula.
Alla prof non interessa che si dimostri (o capisca) come si è arrivati a questa formula, l'importante è credere che sia giusta. Per quanto riguarda la complessità, si tratta di una formula ricorsiva in cui:
- lo spazio usato da ogni ricorsione è lineare alla dimensione della configurazione, quindi è O(f(n));
- il numero di ricorsioni è pari a log(2d*f(n)), quindi O(f(n)).
Ne deriva che la complessità della formula è O(f2(n)), che è polinomiale e quindi soddisfa la seconda condizione da verificare.
Il teorema è dunque dimostrato: TQBF è PSPACE-completo.
Teorema 2 - FORMULA-GAME è PSPACE-completo?
In generale, per gioco si intende una competizione in cui i partecipanti devono raggiungere un certo obiettivo rispettando una serie di regole.
Il FORMULA GAME è un gioco elettrizzante con gli ingredienti giusti per diventare il successo più frizzante dell'estate: quantificatori e valori di verità di formule booleane.
La formula Φ con cui si gioca ha questo aspetto:
Φ = ∃x1 ∀x2 ∃x3 ... Qxk [φ]
, dove Q è un quantificatore universale o esistenziale e φ il resto della formula senza quantificatori (ma con le variabili che si trovano nei loro scope).
Ci sono due giocatori, che giocano a turni alternati:
- giocatore E, che deve dare un valore di verità a tutte le variabili con quantificatore esistenziale. Vince se il valore finale della Φ è pari a 1;
- giocatore A, che deve dare un valore di verità a tutte le variabili con quantificatore universale. Vince se il valore finale della Φ è pari a 0.
Ad esempio, sia data questa formula:
Il giocatore E inizia per primo e dovrà assegnare un valore alla variabile x1. Siccome il suo scopo è fare in modo che la formula risulti pari a 1, per come questa è costruita dovrà riuscire a ottenere un 1 in tutte le sottoformule messe in AND tra loro. Assegnerà x1=1 si assicura un 1 nella prima sottoformula.
Tocca ora ad A, che dovrà intervenire su x2. Il suo scopo è fare in modo che almeno una sottoformula abbia valore 0, così che messa in AND con le altre renda la formula globale pari a 0. Ha senso perciò che assegni x2=0. Si noti però che così facendo ha fatto finire un 1 nella terza sottoformula, in cui era presente la negazione della stessa variabile.
L'ultimo turno spetta ad E, per cui è vita semplice assegnare x3=1 e vincere la partita.
Da tutto questo appare evidente che i giocatori non scelgono a caso i valori, ma adottano una strategia. In particolare diciamo che un giocatore ha una strategia vincente per una partita quando entrambi i contendenti giocano in modo ottimale e riesce comunque a vincere.
Il problema del FORMULA-GAME può essere così definito:
FORMULA-GAME = {φ | il giocatore E ha una strategia vincente nel formula-game associato a φ}
Il teorema da dimostrare è il seguente:
FORMULA-GAME è PSPACE-completo.
Dimostrazione
Invece di dimostrare le due condizioni della PSPACE-completezza possiamo provare a dimostrare che il problema è formulato in modo analogo ad un altro problema PSPACE-completo.
In effetti a pensarci bene FORMULA-GAME è riconducibile a TQBF: la strategia vincente di E è quella che lo porta a rendere la formula pari a 1, esattamente lo stesso scopo di TQFB che vuole che la formula booleana completamente quantificata sia vera. Inoltre in entrambi i casi si interviene sull'assegnamento di valori 0/1 alle variabili, anche se in un caso per vincere e nell'altro per provare la soddisfacibilità.
Poche balle: dato che una formula φ appartiene a TQBF quando φ appartiene a FORMULA-GAME, il teorema è dimostrato dalla stessa dimostrazione di TQBF.
L e NL
Se pensavate che usare spazi lineari poteva soddisfarci vi sbagliavate di grosso. Da questo momento studieremo limiti di spazio sotto-lineari (logaritmici), in cui la macchina legge l'intero ingresso ma non ha spazio sufficiente per memorizzarlo tutto. Va da sé che si tratta di un concetto inapplicabile al tempo, perché significherebbe non avere il tempo di leggere l'intero ingresso.
Per capire meglio la situazione dovremo cambiare modello computazionale: una MdT con due nastri, uno di sola lettura (per gli ingressi) e l'altro di lettura/scrittura (di lavoro). Gli ingressi dovranno rimanere sempre sul primo nastro, mentre sarà quello di lavoro che contruibirà alla spazio complessità della MdT. A queste condizioni possiamo affermare che:
L è la classe di linguaggi che sono decidibili in spazio logaritmico su una MdT deterministica. In altre parole: L=SPACE(logn).
NL è la classe di linguaggi che sono decidibili in spazio logaritmico su una MdT n.d.. In altre parole: NL=NSPACE(logn).
Si noti che il dilemma "L=NL ?" è analogo a quello "P=NP ?".
Esempio L
Come esempio di linguaggio in L consideriamo A={0k1k | k>=0}.
Una MdT che lo descrive potrebbe essere:
M = "su ingresso w: (dove w è una stringa)
1. fai uno scan del nastro e RIFIUTA se c'è uno 0 a destra di un 1;
2. ripeti finché ci sono sia 0 che 1 sul nastro:
3. fai uno scan del nastro, marcando un singolo 0 e un singolo 1;
4. se rimangono degli 0 non marcati mentre tutti gli 1 lo sono (o viceversa),
allora RIFIUTA; altrimenti ACCETTA."
Lo spazio richiesto da M è però lineare al numero di caratteri, quindi non va bene.
Dato però che con una MdT possiamo realizzare qualsiasi funzione eseguibile da un elaboratore, ne potremmo definire una che lavora come contatore. La nostra MdT spazio logaritmica userà allora due contatori, uno per gli 0 e uno per gli 1, e scriverà i risultati sul nastro di lavoro per fare un confronto: se i numeri sono uguali, allora ACCETTA; altrimenti RIFIUTA. Rispetta i requisiti di L? Sì, perché la rappresentazione in binario del numero che quantifica la dimensione di una stringa di caratteri (gli 0 e gli 1) è logaritmica alla dimensione stessa. Sopracciglio alzato? Facciamo un esempio di stringa di 30 caratteri, e subito sotto il numero binario che ne indica la dimensione:
000000000000000000000000000000
11110
Un bel risparmio di spazio, no?!
Quindi A appartiene alla classe L.
Esempio NL
Nel capitolo sulla Complessità nel tempo abbiamo dimostrato che il problema PATH è in P. Ora vogliamo vedere se è anche in NL.
Dato un grafo diretto G, il problema PATH ha come obiettivo quello di determinare se esiste un percorso diretto tra due nodi s e t. Più formalmente:
PATH = {<G,s,t> | G è un grafo diretto che ha percorso diretto tra s e t}
Supponiamo di avere una MdT n.d., e selezioniamo in modo n.d. un nodo collegato ad s, memorizzandolo (solo lui) sul nastro. Ripetiamo l'operazione sull'ultimo nodo selezionato, andando a sovrascrivere l'identificativo del nuovo nodo estratto in modo n.d.. Continuiamo a ciclare finché non si è raggiunto il nodo t, o finché il numero di iterazioni non sia maggiore del numero dei nodi (così da escludere loop infiniti su un percorso).
Questo algoritmo garantisce la soluzione del problema in uno spazio logaritmico, quindi PATH è in NL.
NL-completezza
..to be continued
Changed line 107 from:
Facciamo un esempio di risoluzione. Dati in ingresso x=24 e y=18:
to:
Facciamo un esempio di risoluzione. Dati in ingresso x=24 e y=18:\\
Changed lines 141-170 from:
to:
Sappiamo già dalle lezioni precedenti che i linguaggi liberi dal contesto (da ora CFL) sono decidibili, perché è possibile creare un algoritmo che lo decida. Dobbiamo quindi dimostrare che tale algoritmo viene eseguito in tempo polinomiale. Dov'è la fregatura? Che la dimostrazione della decidibilità di un CFL L tirava in ballo il fatto che era stato generato da una grammatica libera dal contesto G espressa nella forma normale Chomsky, e che bisognava verificare tutte le derivazioni di G per vedere se una certa stringa di L poteva essere accettata. Il numero di derivazioni è ahinoi esponenziale, quindi dobbiamo scegliere un'altra strada per dimostrare il nostro teorema.
Chi di noi non stava pensando alla programmazione dinamica come soluzione? Esatto.
Nella programmazione dinamica si cercano e si utilizzano le soluzioni di sottoproblemi per risolvere il problema principale. Nel nostro caso i sottoproblemi sono le sottostringhe generate per scomposizione dall'originale stringa w generata da G, e dovremo verificare che ognuna di esse possa essere derivata a partire dalle variabili della grammatica. Per fare ciò costruiremo una tabella n x n, con coordinate i e j. In ogni cella (i,j) con i<=j potrò trovare tutte le variabili che mi permettono di generare la sottostringa wiwi+1...wj; al contrario tutte le celle con i>j saranno inutilizzate. Grazie ai principi della programmazione dinamica useremo via via le soluzioni ottenute per le sottostringhe precedenti. Come? Quando andando avanti con la risoluzione scopro che una data (i,j) potevo generarla utilizzando una sottostringa già risolta, nella cella metto quella sottostringa. Come? Ogni sottostringa di lunghezza k+1 può essere divisa in k modi possibili (ad esempio w1w2w3w4 può essere divisa in: w1|w2w3w4, w1w2|w3w4, w1w2w3|w4). Per riutilizzare le informazioni già messe in tabella basterà cercare nella mia grammatica una regola A->BC dove B mi permette di generare la parte sinistra e C la destra.
Ed ora, vediamo la MdT D che fa tutto questo (con "subs" si intenderà "sottostringa"):
D = "su ingresso w=w1...wn:
1. se w=ε ed S->ε è una regola, ACCETTA;
2. ripeti da i=1 ad i=n:
3. per ogni variabile A:
4. verifica se A->b è una regola, dove b=wi;
5. se sì, inserisci A nella tabella alle coordinate (i,i);
6. ripeti da l=2 ad l=n: (l è la lunghezza della subs)
7. ripeti da i=1 ad i=n-l+1: (i è la posizione iniziale della subs)
8. sia j=i+l-1; (j è la posizione finale della subs)
9. ripeti da k=i a k=j-1: (k è la posizione della separazione)
10. per ogni regola A->BC:
11. se la cella (i,k) contiene B e la cella (k+1,j) contiene C, allora metti A nella cella (i,j)
12. se S è nella cella (1,n) ACCETTA; altrimenti RIFIUTA."
In altre parole, se nell'ultima colonna della prima riga ci ritroviamo la variabile iniziale S l'algoritmo ha successo. Via quelle sopracciglia alzate, facciamo piuttosto l'analisi dell'algoritmo considerando i passaggi più critici:
- (4) e (5) possono essere ripetuti al più n*v volte, dove v è il numero di variabili della grammatica. Dato che v è comunque una costante (non dipende dalla n), entrambi i passi hanno complessità O(n);
- (6) può essere svolto al più n volte, quindi è O(n);
- (7) viene ripetuto al più n volte tutte le volte che viene eseguito (6), quindi avrà complessità O(n)*n =O(n2);
- (8) e (9) vengono ripetuti al più n volte tutte le volte che viene eseguito (7), quindi avranno complessità O(n2)*n =O(n3);
- (10) e quindi (11) vengono eseguiti ogni volta che partono (8) e (9), e vengono ripetuti r volte, dove r è il numero di regole. Avranno quindi complessità O(n3)*r=O(n3) (perché r è costante).
La complessità totale dell'algoritmo sarà dunque O(n)+O(n3)=O(n3), che è meravigliosamente polinomiale. Quindi abbiamo dimostrato che ogni linguaggio libero dal contesto è in P.
Added lines 1-144:
(:title Informatica Teorica - Complessità nel tempo:)
Torna alla pagina di Informatica Teorica
:: Informatica Teorica - Complessità nel tempo ::
Appunti & Dimostrazioni del 5 Maggio
Cenni teorici
Sia M una Macchina di Touring (da ora MdT) deterministica che si ferma su ogni ingresso. Il tempo di esecuzione o complessità nel tempo di M è la funzione f: N -> N, dove f(n) è il numero massimo di passi che M impiega su ogni ingresso di lunghezza n. Se f(n) è il tempo di esecuzione di M, diciamo che M è eseguita in tempo f(n) e che M è una tempo f(n) MdT.
Della complessità nel tempo non si dà una misura precisa, ma una stima risultante dall'analisi asintotica dell'algoritmo. In particolare introduciamo le notazioni O ("o grande") e o ("o piccolo").
Siano f e g due funzioni f,g: N -> R+. Diciamo che f(n) = O(g(n)) se esistono due interi positivi c e n0 tali che per ogni intero n>=n0:
f(n) >= c*g(n)
Quando f(n) = O(g(n)) diciamo che g(n) è un limite superiore (upper bound) per f(n), o più precisamente che g(n) è un limite superiore asintotico per f(n), per enfatizzare il fatto che stiamo ignorando le costanti.
Se O può essere definita come una funzione asintoticamente "non maggiore" di un'altra (minore o uguale), con o piccolo definiamo una funzione asintoticamente "minore" di un'altra (strettamente minore). Facendo qualche esempio:
- n = o(nlog(logn))
- nlog(logn) = o(n(logn))
- n2 = o(n3)
Perché abbiamo parlato di o grandi e o piccole? Perché quando si fa l'analisi asintotica di un algoritmo si considerano solo i termini di ordine maggiore che partecipano a formare il tempo di esecuzione complessivo, trascurando i coefficienti, le costanti e tutti i termini di grado inferiore.
Ad esempio: f(n) = 3n3 + 2n2 + n + 100 = O(n3)
Concludiamo definendo cos'è una classe di complessità nel tempo:
Sia t:N->R+ una a funzione. Definiamo la classe di complessità nel tempo, TIME(t(n)), come l'insieme di tutti i linguaggi che sono decidibili in tempo O(t(n)) (polinomiale) da una MdT.
Teorema 1 - sulle relazioni di complessità tra modelli
Sia t(n) una funzione, con t(n)>=n. Ogni MdT multinastro t(n)-tempo ha una equivalente MdT a nastro singolo O(t2(n))-tempo.
Dimostrazione
Consideriamo M una MdT con k nastri, ed S la corrispondente MdT a nastro singolo. S è costruita copiando i contenuti dei k nastri sul suo mettendoli in fila uno dopo l'altro e separandoli con un #. Perché S riesca a simulare un singolo passo di M su un certo nastro, dovrà prima posizionare la propria testina sul punto corrispondente, e solo dopo compiere l'operazione. Sappiamo dal testo del teorema che nel peggiore dei casi la testina di M impiegherà t(n) tempo per raggiungere il punto desiderato e compiere l'operazione, quindi avrà complessità O(t(n)). La complessità di S sarà dunque data dai contributi derivanti dalle seguenti operazioni:
- ricopiare correttamente il contenuto di M, impiegando O(n) passi
- simulare M su nastro singolo, impiegando t(n) passaggi ognuno con complessità O(t(n)). Ovvero: t(n)*O(t(n))=O(t2(n))
Dato che tra O(n) e O(t2(n)) il secondo è il contributo più importante, trascuriamo il primo è affermiamo che simulare una multinastro su MdT a nastro singolo richiede il quadrato del tempo di esecuzione.
Teorema 2 - sulle relazioni di complessità tra modelli
Sia t(n) una funzione, con t(n)>=2. Ogni MdT a singolo nastro non-deterministica t(n)-tempo ha una equivalente MdT a nastro singolo deterministica 2O(t(n))-tempo.
Dimostrazione
Data una MdT non deterministica N con tempo di esecuzione t(n), sappiamo che è possibile creare una MdT deterministica D equivalente che intraprende ogni possibile ramo della computazione non deterministica. In particolare, dato un ingresso di lunghezza n (la grandezza della stringa w) ogni ramo dell'albero di computazione non deterministica di N avrà al massimo lunghezza t(n). Supponendo che ogni nodo possa avere al massimo b figli (ovvero le scelte legali della funzione di transizione), avremo al massimo bt(n) foglie.
Per rendere più efficiente l'algoritmo, l'esplorazione dell'albero alla ricerca dello stato di accettazione non viene fatta in profondità (dalla radice alla foglia e poi da capo con un altro percorso), ma in ampiezza (controllando gli stati dei nodi livello per livello).
Il numero di nodi nell'albero è di poco inferiore al doppio delle foglie, quindi possiamo dare come limite superiore al numero di nodi O(bt(n)). A questo punto, sapendo che il tempo di esplorazione dalla radice a qualunque nodo è pari a O(t(n)), e che nel caso peggiore bisognerà visitare tutti gli O(bt(n)) nodi dell'albero, il tempo totale di esecuzione dell'algoritmo D è pari a:
O(t(n)*bt(n)) = 2O(t(n))
Facciamo qualche considerazione conclusiva sull'equivalenza O(t(n)*bt(n))=2O(t(n)):
- si tratta di un prodotto tra un polinomio e un'esponenziale, ed avendo quest'ultimo un ordine di grandezza maggiore, è possibile trascurare il primo e considerare come complessità dell'algoritmo solo O(bt(n))
- per una serie di motivi che non ci interessano (che riguardano comunque la teoria della complessità), è possibile passare da O(bt(n)) a O(2t(n))
- siccome la base 2 è una costante, possiamo portare in alto l'o grande: O(2t(n))=2O(t(n))
Il teorema sembra già dimostrato, ma in realtà non va dimenticato che la D che simula N non è più una MdT a singolo nastro, ma per costruzione ne ha 3. Poco male: dal Teorema 1 sopra riportato sappiamo che ogni MdT multinastro t(n)-tempo ha una equivalente MdT a nastro singolo O(t2(n))-tempo. Quindi:
(2O(t(n)))2 = 2O(2t(n)) = 2O(t(n))
Dimostrazione conclusa.
Classe P
Introduciamo ora la classe P, ovvero la classe dei linguaggi che sono decidibili in tempo polinomiale su una MdT deterministica a singolo nastro. Si tratta di una classe matematicamente robusta, che non dipende quindi dal modello computazionale che sceglieremo per risolvere il problema.
I problemi in P, o tempo-polinomiali, sono una classe di problemi realisticamente risolvibili con un calcolatore. Per dimostrare che un problema è tempo-polinomiale bisognerà prima dare un limite polinomiale superiore (in notazione O grande) per il numero di passi che l'algoritmo usa per un ingresso di lunghezza n, poi esaminare ogni passo della descrizione dell'algoritmo per assicurarci che ogni passo sia tempo-polinomiale.
PATH è P?
Dato un grafo diretto G, il problema PATH ha come obiettivo quello di determinare se esiste un percorso diretto tra due nodi s e t. Più formalmente:
PATH = {<G,s,t> | G è un grafo diretto che ha percorso diretto tra s e t}
Per dimostrare che PATH appartiene a P dovremo dimostrare che è risolvibile in tempo polinomiale. Una possibile strada è quella di partire da s e marcare tutti i nodi raggiungibili con passo 1, quindi ripetere l'operazione a partire da essi (raggiungendo una distanza da s pari a 2). L'operazione va ripetuta finché non è più possibile marcare nuovi nodi. A questo punto bisogna verificare se t è stato segnato o no: se sì PATH è vero, altrimenti no.
Costruiamo ora la MdT deterministica M che implementa l'algoritmo:
M = "su ingresso <G,s,t>:
1. marca s;
2. ripeti finché non abbiamo nuovi nodi da marcare:
3.fai una scan degli archi di G. Se trovi l'arco (a,b), dove a è un nodo marcato e b no, marca b;
4. se t è marcato, allora ACCETTA; altrimenti RIFIUTA."
Facciamo l'analisi dell'algoritmo:
- i passi (1) e (4) sono ripetuti una sola volta
- i passi (2) e (3) (il loop) sono eseguiti m volte, dove m è il numero di nodi
Quindi, dato che il numero di passi è 1+1+m e che ognuno di essi ha complessità polinomiale, PATH è in P.
RELPRIME è P?
Prima di tutto, di cosa diavolo stiamo parlando? Il problema RELPRIME è quello che deve verificare se due numeri sono primi tra loro, ovvero se il più grande intero che li divide entrambi è 1. Più formalmente:
RELPRIME = {<x,y> | x e y sono primi tra loro}
Per dimostrare che RELPRIME appartiene a P dobbiamo trovare una MdT deterministica che lo risolva in tempo polinomiale. Iniziamo a scrivere una MdT che calcoli il divisore maggiore dati due interi x e y:
E = "su ingresso <x,y>:
1. ripeti finché y=0;
2. assegna a x il valore x mod y;
3. scambia x e y;
4. output: x"
Facciamo un esempio di risoluzione. Dati in ingresso x=24 e y=18:
(1)
(2) x = 24 mod 18 = 6
(3) x = 18 , y = 6
(1) y=0? NO
(2) x = 18 mod 6 = 0
(3) x = 6 , y = 0
(1) y=0? SÌ
(4) output: 6
Creiamo ora una seconda MdT che usa E come subroutine:
R = "su ingresso <x,y>:
- esegui E su ingresso <x,y>;
- se il risultato è 1, allora ACCETTA; altrimenti RIFIUTA."
Per fare l'analisi dell'algoritmo E, consideriamo due casi:
- se (x/2) >= y, dato che (x mod y) < y, avremo che:
(x mod y) < y <= (x/2)
- se (x/2) < y, dato che (x mod y) = x - y, avremo che:
(x mod y) = x - y <= (x/2)
In entrambi i casi avremo che ad ogni passata del ciclo il valore della x viene come minimo dimezzato. Quindi il numero massimo di volte in cui vengono ciclati i passi (2) e (3) di E è il valore più piccolo tra 2logx e 2logy. Essendoci di messo un logaritmo il numero di passi è sicuramente polinomiale, ed essendo ogni operazione di complessità polinomiale il problema RELPRIME è sicuramente in P.
Teorema 3 - sui linguaggi liberi dal contesto
Ogni linguaggio libero dal contesto è membro di P.
Dimostrazione
..to be continued
Torna alla pagina di Informatica Teorica
|
|