Torna alla pagina di Informatica Teorica

 :: Informatica Teorica - Automi a pila ::

Appunti & Dimostrazioni del 14 Aprile

Concetti iniziali

Nel capitolo precedente abbiamo imparato che una CFG è in grado di costruire un linguaggio libero dal contesto (da ora, anche CFL). Ora introduciamo un nuovo tipo di modello computazionale che si occupa di riconoscere i linguaggi, ovvero l' automa a pila (PDA, Push-Down Automata).
L'automa a pila è molto simile agli automi non deterministici, ma ha un optional che tutti gli NFA gli invidiano: lo stack, che fornisce memoria aggiuntiva al PDA, permettendogli di riconoscere anche i linguaggi non regolari.
Dato che l'automa a pila ha la stessa potenza descrittiva di una CFG, potremo usarlo per dimostrare che un certo linguaggio è libero dal contesto. E' un'equivalenza importante, perché alcuni linguaggi sono più semplici da descrivere in termini di riconoscimento che di generazione.

Ecco un confronto tra gli schemi di un NFA e un PDA:

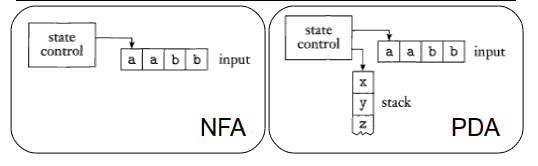
Lo state control rappresenta gli stati e le funzioni di transizione, il nastro rappresenta le stringhe in ingresso, mentre le frecce rappresentano la testina dell'ingresso, che punta al prossimo simbolo che deve essere letto. Nel PDA fa la sua bella comparsa anche lo stack, su cui il PDA può scrivere e leggere simboli in modalità "last in, first out". La scrittura sullo stack è chiamata pushing, e consiste nell'inserimento di un nuovo simbolo nella posizione in cima alla pila, spingendo giù tutti gli altri di una posizione; la lettura invece è detta popping e consiste nell'estrazione del simbolo in prima posizione, che viene appunto letto e rimosso. Si noti che lo stack può contenere una quantità illimitata di informazioni, quindi ad esempio sarà in grado di riconoscere un linguaggio non regolare come: {0ⁿ1ⁿ|n>=0}. Come? Basterà leggere un simbolo da input e pushare ogni 0 letto nello stack (che è illimitato); quando poi arriveremo agli 1, farà il popping di uno 0 per ogni 1 letto, e se alla fine dei giochi lo stack è vuoto allora l'ingresso sarà accettato.

Concludiamo la panoramica iniziale sottolineando che l'automa a pila può essere sia deterministico che n.d., che non sono equivalenti in termini di potenza: il PDA n.d. riconosce molti più linguaggi dell'altro.

Definizione formale di automa a pila

La definizione formale di automa a pila è molto simile a quella dell'automa a stati finiti, con l'unica eccezione della presenza dello stack, che può avere un alfabeto diverso rispetto a quello d'ingresso.

Definizione formale di computazione

Siano dati:

• un automa a pila M=(Q,Σ,Γ,δ,q₀,F)
• una stringa di ingresso w tale che w = w₁w₂..w_m , dove ogni w_i fa parte dell'alfabeto Σ_ε
• una stringa s tale che s = s₁s₂..s_m , dove ogni s_i appartiene allo stack

Diciamo allora che M accetta w se esiste una sequenza di stati r₀r₁..r_m in Q che rispettino tre condizioni:

1. r₀ = q₀ e s₀ = ε (la macchina parte dallo stato iniziale e con lo stack vuoto);
2. per ogni i = 0, .. , m-1, abbiamo che (r_i+1,b) ∈ δ(r_i,w_i+1,a), dove s_i=at e s_i+1=bt per qualche a e b che appartengono a Γ_ε e con t∈ Γ* (lo stato futuro di M dipende dallo stato attuale, dal simbolo in ingresso e dall stack);
3. r_m ∈ F (la macchina accetta l'ingresso se l'ultimo stato in cui finisce è tra quelli finali).

Esercizietto

Dare la definizione formale del PDA che riconosce il linguaggio {0ⁿ1ⁿ|n>=0}.

Soluzione

Qualche riga fa avevamo fatto una descrizione alla buona di come avrebbe dovuto comportarsi un automa a pila per riconoscere il linguaggio. Cerchiamo ora di dare una spiegazione più seria.
La lettura dei simboli in ingresso da parte del PDA può essere distinta in due fasi:

1. finché il simbolo letto è uno 0, verrà messo in cima allo stack;
2. quando il simbolo letto diventa un 1, verrà fatto il pop di uno 0 dallo stack per ogni simbolo 1 letto.

Se la lettura della stringa in ingresso finisce in concomitanza con lo svuotamento completo dello stack, allora la stringa è accettata; altrimenti è rifiutata.

Cominciamo ora con le definizioni formali.
Sia dato un automa a pila M=(Q,Σ,Γ,δ,q₁,F), dove:

• Q = {q₁, q₂, q₃, q₄}
• Σ = {0,1}
• Γ = {0,$} (dove il simbolo di $ ci servirà per capire se lo stack è vuoto)
• q₁ è lo stato iniziale
• F = {q₁,q₄} (anche q₁ è stato finale perché potremmo passare all'automa una stringa vuota)
• δ è data dalla seguente tabella:

Il comportamento di questo PDA si capisce meglio rappresentandolo con un più familiare diagramma degli stati:

Come interpretare le frecce? Ad esempio, a,b -> c va letto come: quando l'automa legge il simbolo a dall'ingresso, dovrà sostituire il simbolo b che si trova in cima allo stack con il simbolo c. In pratica b si riferisce a un pop e c a un push.
Riferendoci al diagramma degli stati, vediamo come si comporta l'automa:

• da q₁ a q₂: ε,ε->$
  Prima di leggere qualsiasi simbolo della stringa, pushiamo nello stack vuoto il simbolo $ (presto capiremo perché)
• da q₂ a q₂: 0,ε->0
  Rimaniamo in q₂ finché leggiamo il simbolo 0 dalla stringa in ingresso. Per ognuna di queste letture inseriamo uno 0 in cima allo stack (senza sostituirlo con niente)
• da q₂ a q₃: 1,0->ε
  Quando ci arriva il primo 1, passiamo dallo stato q₂ al q₃. Per quanto riguarda lo stack facciamo un pop del primo 0 e non ci scriviamo niente
• da q₃ a q₃: 1,0->ε
  Rimaniamo in q₃ finché leggiamo il simbolo 1 dalla stringa in ingresso. Per ognuna di queste letture facciamo un pop di uno 0 dallo stack
• da q₃ a q₄: ε,$->ε
  Quando finiamo i simboli da leggere in ingresso, se in cima alla lista ritroviamo il simbolo $ possiamo affermare che lo stack si è svuotato, quindi possiamo passare allo stato finale q₄

Teorema 1 - sull'equivalenza con CFG

A inizio capitolo abbiamo detto che l'automa a pila ha la stessa potenza descrittiva di un CFG. Non l'avessimo mai fatto: ora ci tocca dimostrarlo.

Dimostrazione

Il teorema è un "se e solo se", quindi vanno dimostrati entrambi i sensi delle implicazioni.

(I) Se un linguaggio è libero dal contesto, allora esiste un PDA che lo riconosce

Dato che per definizione un CFL è generato da una grammatica libera dal contesto, non dobbiamo fare altro che dimostrare che ogni CFG G può essere convertita in un equivalente PDA P. In pratica dobbiamo costruire P in modo che se gli passiamo in ingresso una stringa w generata da G, questi dovrà accettarla. Ma come fa a capire se è davvero generata dalla grammatica a lui equivalente? Dovrà verificare (in modo n.d. se tra tutte le derivazioni possibili della grammatica ne esiste una che dalla variabile iniziale porta a w.
Più nel dettaglio, P comincia la sua computazione scrivendo la variabile iniziale sullo stack; poi prosegue attraverso una serie di stringhe intermedie ottenute sostituendo le variabili secondo le regole della grammatica; infine quando arriva a una stringa composta da soli terminali la confronta con w: se corrispondono allora P accetta, altrimenti abbandona quel ramo della computazione.
Tutto ciò è molto bello, ma dove le memorizzo le stringhe intermedie? Anche se la tentazione è forte, non posso metterle così come sono nello stack. Se infatti dovessi fare una sostituzione di una variabile in una stringa intermedia e questa non si trova in cima allo stack, dove pensate che la prenderemo? Esatto, proprio là dietro. La soluzione è conservare solo una parte della stringa intermedia nello stack, quella che va dalla prima variabile in poi; tutti i simboli che vengono prima devono corrispondere con la stringa in ingresso, altrimenti buttiamo via tutto.

Siamo pronti.
Sia dato l'automa a pila P=(Q,Σ,Γ,δ,q₁,F). Per rendere la costruzione più chiara, descriveremo la funzione di transizione con la notazione breve, che permette di scrivere sullo stack una stringa intera con un unico passo della macchina (normalmente invece per scriverci su una stringa di dieci caratteri, ad esempio ACCABANANA, dovremmo fare 10 passi).
I tre stati fondamentali di P sono Q={q_start, q_loop, q_accept}, in cui q_start è quello iniziale e q_accept l'unico accettato. Diamo ora una descrizione del funzionamento di P:

1. δ(q_start,ε,ε)={(q_loop,S$)}
   "metti il simbolo $ e la variabile iniziale nello stack, quindi vai in q_loop";
2. continua a ripetere i seguenti passi:
   1. δ(q_loop,ε,A)={(q_loop,w) | dove A->w è una regola in R}
      "se in cima allo stack c'è una variabile A, seleziona in modo non deterministico una delle regole per A e sostituisci A con la stringa che si trova a destra della regola";
   2. δ(q_loop,a,a)={(q_loop,ε)}
      "se in cima allo stack c'è un simbolo terminale a, leggi il prossimo simbolo dall'ingresso e confrontalo con a. Se corrispondono, ripeti; altrimenti abbandona questo ramo della computazione non deterministica";
   3. δ(q_loop,ε,$)={(q_accept,ε)}
      "se in cima allo stack c'è il simbolo $, entra nello stato di accettazione!" (quando si arriva a $ abbiamo infatti la garanzia di aver letto tutta la stringa w)

Ed ecco finalmente il diagramma degli stati di P in tutta la sua fierezza:

(II) Se un PDA riconosce un linguaggio, allora è un linguaggio libero dal contesto

Situazione inversa: abbiamo un PDA P e vogliamo creare un CFG G che generi tutte le stringhe accettate da P. Seguitemi prima con la costruzione, poi verificheremo se ci aiuta a dimostrare l'implicazione (tenetevi pronti: ci sarà un altro "se e solo se" da affrontare).

Come prima cosa, dovremo aggiungere alla nostra grammatica G una variabile A_pq per ogni coppia di stati p e q in P. Non è una variabile a caso, ma quella che genera tutte le stringhe che possono portare il PDA da p a q lasciando lo stack nelle stesse condizioni in cui lo si è trovato (o vuoto o con lo stesso contenuto). Per riuscirci, dobbiamo fornire a P tre nuove caratteristiche:

1. deve avere un unico stato accettante q_accept;
2. deve svuotare il suo stack prima di accettare;
3. ogni transizione deve consistere o in un'operazione di push o in una di pop, non entrambe (basta dividere la transizione in due).

Qualcosa sul comportamento di P già si capisce da queste caratteristiche: la prima operazione su una qualsiasi stringa x sarà di push, e l'ultima di pop. E le altre? Distinguiamo due casi:

• il simbolo estratto dallo stack alla fine della computazione è quello che avevo messo all'inizio, quindi lo stack è vuoto solo in questi due momenti. Simuliamo questa eventualità con la regola:
  A_pq->aA_rsb

• seconda situazione: il simbolo estratto dallo stack alla fine della computazione non è quello che avevo messo all'inizio, quindi lo stack si è svuotato completamente tra p e q almeno una volta, in uno stato che chiameremo r. Per questa eventualità introduciamo la regola:
  A_pq->A_prA_rq

La costruzione di G termina aggiungendo per ogni p ∈ Q la regola: A_pp->ε.

La costruzione è questa, ma per dimostrare la seconda implicazione del Teorema 1 (ve lo ricordate ancora?) dovremo dimostrare che A_pq genera una stringa x se e solo se x può portare P da p con stack vuoto a q con stack vuoto. Distinguiamo ancora i due versi dell'implicazione.

(II.a) Se A_pq genera x, allora x può portare P da p con stack vuoto a q con stack vuoto
La dimostrazione viene fatta per induzione.

• passo base:
  La derivazione ha un solo passo, quindi nella parte destra della regola devono esserci solo terminali. L'unica regola di questo tipo in G è A_pp->ε, che è verificata perché se non prendo niente in ingresso parto con lo stack vuoto e finisco con lo stack vuoto.
• passo induttivo:
  Consideriamo vere le derivazioni con al più k passi, con k>=1, e verifichiamo se sono vere anche per k+1 passi.
  Supponiamo di avere A_pq-*->x ("A_pq deriva x") in k+1 passi. Come abbiamo visto, nel primo passo di derivazione sono due le regole che possono essere applicate:
  1. A_pq->aA_rsb
     Consideriamo una porzione y della x generata da A_rs, tale che x=ayb. Dato che A_rs-*->y in k passi, l'ipotesi induttiva ci dice che P può andare da r con stack vuoto ad s con stack vuoto. Vediamo bene cosa succede: P parte da p con lo stack vuoto, e dopo aver letto a va nello stato r mettendo t in cima allo stack; poi P legge la stringa y che lo porta allo stato s lasciando t lì dov'è; infine P legge b che lo porta allo stato q facendogli fare un pop di t dallo stack. Perfetto: parto e arrivo con lo stack vuoto;
  2. A_pq->A_prA_rq
     Consideriamo le porzioni y e z delle x che generano rispettivamente A_pr e A_rq, tali che x=yz. Dato che A_pr-*->y e A_rq-*->z in massimo k passi, l'ipotesi induttiva ci dice che y può portare P da p ad r con lo stack vuoto all'inizio e alla fine; stessa cosa per z che porta P da r a q. Quindi, sommando gli effetti, x può portare P dallo stato p con stack vuoto allo stato q con stack vuoto. Perfetto, abbiamo completato il passo induttivo!

(II.b) Se x può portare P da p con stack vuoto a q con stack vuoto, allora A_pq genera x''
Anche in questo caso la dimostrazione va fatta per induzione.

• passo base:
  La computazione ha 0 passi, quindi stato iniziale e stato finale coincidono. Chiamiamo p questo stato, per cui vale la regola A_pp-*->x. Ma dato che in 0 passi P può leggere solo la stringa vuota, allora x=ε; sostituiamo il valore di x nella regola di prima e otteniamo A_pp->ε, che è una regola di G per costruzione! La base è provata!
• passo induttivo:
  Consideriamo vere le computazioni con al più k passi, con k>=0, e verifichiamo se sono vere anche per k+1 passi.
  Se supponiamo che P abbia una computazione in cui x porta p a q con stack vuoto in k+1 passi, i casi sono due:
  1. "lo stack è vuoto solo all'inizio e alla fine della computazione"
     Chiamiamo t il simbolo che metto in cima allo stack alla prima mossa e che tolgo solo all'ultima. Sia a l'ingresso letto al primo passo, b quello letto all'ultimo, r lo stato in cui vado dopo la prima mossa, ed s lo stato che precede l'ultima. Abbiamo quindi che δ(p,a,ε) contiene (r,t) e δ(s,b,t) contiene (q,ε), perciò la regola A_pq->aA_rsb è in G.
     Se adesso chiamiamo y la parte di x priva dei simboli a e b (dove x=ayb), l'ingresso y può portare P dallo stato r ad s senza andare a toccare il simbolo t nello stack; in altre parole se diamo y in ingresso a P, questo può andare da r con lo stack vuoto ad s con lo stack vuoto. Evitando di considerare a e b abbiamo rimosso due passaggi dai k+1 necessari per la computazione di x, quindi y richiede k-1 passi. Non chiedetemi perché, ma era proprio quello che volevamo sentirci dire! Grazie all'ipotesi induttiva possiamo infatti affermare che A_rs-*->y, e di conseguenza che A_pq-*->x!
  2. "lo stack è vuoto all'inizio e alla fine della computazione, e anche in un altro punto"
     Sia r lo stato, diverso da quello iniziale e finale, in cui lo stack è vuoto; quindi le parti di computazione che vanno da p ad r e da r a q impiegano al massimo k passi. Chiamiamo ora y l'ingresso letto da P nella prima parte z quello letto nella seconda. L'ipotesi induttiva ci dice che A_pr-*->y e che A_rq-*->z. Ma dato che la regola A_pq->A_prA_rq è in G, A_pq-*->x, e quindi abbiamo completato il passo induttivo.

Quindi, ricapitoliamo. Dovevamo dimostrare questo teorema:

Avendo dimostrato tutti i possibili "se e solo se" nei casi (I), (II.a) e (II.b), possiamo finalmente dire che 'sto teorema immondo è dimostrato!

Corollario al Teorema 1

Ebbene sì, quell'incubo aveva anche un corollario:

Esticazzi.

Torna alla pagina di Informatica Teorica